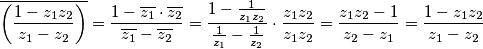Šećer na kraju, jedan više teorijski zadatak.
Primjer. 5. Neka su 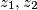 međusobno različiti kompleksni brojevi modula
međusobno različiti kompleksni brojevi modula  . Dokažite da je
. Dokažite da je 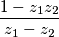 realan broj.
realan broj.
Rješenje. Kao i inače, možemo na to lupit 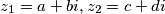 te
te 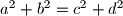 , ali ne budemo uvijek takve sreće, a i meni se neda to rješenje pisat. Makar, bitno je naglasit, ako ne vidite bolji način vrijedi i to isprobat, i ako ne uspijete možda pokupite koje bodove. Dugo, naporno rješenje je i dalje rješenje, pogotovo ako nemate druge ideje.
, ali ne budemo uvijek takve sreće, a i meni se neda to rješenje pisat. Makar, bitno je naglasit, ako ne vidite bolji način vrijedi i to isprobat, i ako ne uspijete možda pokupite koje bodove. Dugo, naporno rješenje je i dalje rješenje, pogotovo ako nemate druge ideje.
No, srećom, i za vas čitatelje, a i za mene, postoji elegantnije rješenje uz malo teorije i dosta manje algebre nego brute force način. Naime, negdje u uvodu sam spomenuo da je broj  realan ako i samo ako je
realan ako i samo ako je 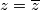 . Probat ćemo to iskoristiti.
. Probat ćemo to iskoristiti.
Odredimo što je 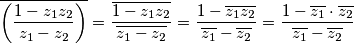
Sada još kako je 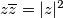 dobijemo
dobijemo 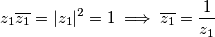 te analogno za
te analogno za 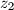 .
.
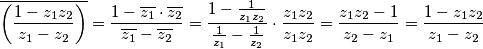
Stoga to zaista jest realan broj.
Kako biste dobili bod na ovom zadatku kao rješenje upišite 5.
Šećer na kraju, jedan više teorijski zadatak.
\textit{Primjer. 5.} Neka su $z_1,z_2$ međusobno različiti kompleksni brojevi modula $1$. Dokažite da je
$$\frac{1-z_1z_2}{z_1-z_2}$$ realan broj.
\textit{Rješenje.} Kao i inače, možemo na to lupit $z_1=a+bi,z_2=c+di$ te $a^2+b^2=c^2+d^2$, ali ne budemo uvijek takve sreće, a i meni se neda to rješenje pisat. Makar, bitno je naglasit, ako ne vidite bolji način vrijedi i to isprobat, i ako ne uspijete možda pokupite koje bodove. Dugo, naporno rješenje je i dalje rješenje, pogotovo ako nemate druge ideje.
No, srećom, i za vas čitatelje, a i za mene, postoji elegantnije rješenje uz malo teorije i dosta manje algebre nego brute force način. Naime, negdje u uvodu sam spomenuo da je broj $z$ realan ako i samo ako je $z=\overline{z}$. Probat ćemo to iskoristiti.
Odredimo što je
$$\overline{\left(\frac{1-z_1z_2}{z_1-z_2}\right)}=\frac{\overline{1-z_1z_2}}{\overline{z_1-z_2}}=\frac{1-\overline{z_1z_2}}{\overline{z_1}-\overline{z_2}}=\frac{1-\overline{z_1}\cdot\overline{z_2}}{\overline{z_1}-\overline{z_2}}$$
Sada još kako je $z\overline{z}=\lvert z\rvert^2$ dobijemo
$$z_1\overline{z_1}=\lvert z_1\rvert^2=1\implies \overline{z_1}=\frac{1}{z_1}$$ te analogno za $z_2$.
$$\overline{\left(\frac{1-z_1z_2}{z_1-z_2}\right)}=\frac{1-\overline{z_1}\cdot\overline{z_2}}{\overline{z_1}-\overline{z_2}}=\frac{1-\frac{1}{z_1z_2}}{\frac{1}{z_1}-\frac{1}{z_2}}\cdot\frac{z_1z_2}{z_1z_2}=\frac{z_1z_2-1}{z_2-z_1}=\frac{1-z_1z_2}{z_1-z_2}$$
Stoga to zaista jest realan broj.
Kako biste dobili bod na ovom zadatku kao rješenje upišite 5.
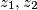 međusobno različiti kompleksni brojevi modula
međusobno različiti kompleksni brojevi modula  . Dokažite da je
. Dokažite da je 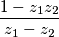 realan broj.
realan broj.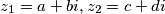 te
te 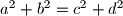 , ali ne budemo uvijek takve sreće, a i meni se neda to rješenje pisat. Makar, bitno je naglasit, ako ne vidite bolji način vrijedi i to isprobat, i ako ne uspijete možda pokupite koje bodove. Dugo, naporno rješenje je i dalje rješenje, pogotovo ako nemate druge ideje.
, ali ne budemo uvijek takve sreće, a i meni se neda to rješenje pisat. Makar, bitno je naglasit, ako ne vidite bolji način vrijedi i to isprobat, i ako ne uspijete možda pokupite koje bodove. Dugo, naporno rješenje je i dalje rješenje, pogotovo ako nemate druge ideje. realan ako i samo ako je
realan ako i samo ako je 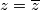 . Probat ćemo to iskoristiti.
. Probat ćemo to iskoristiti.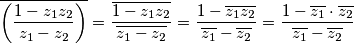
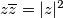 dobijemo
dobijemo 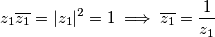 te analogno za
te analogno za 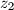 .
.