Dobrodošli u 6. tjedan tečaja. Tema ovog tjedna su kongruencije i njihova svojstva, tj. područje kojim se bavimo je teorija brojeva. Ako čitate ove primjere, nadam se da ste već pogledali uvodno predavanje profesorice Zelčić. Ovdje ćemo samo proći neka dodatna svojstva kongruencija te par primjera. Ako želite pogledati nešto o osnovnim svojstvima u tekstualnom obliku, preporučujem ovaj dokument.
Sada pređimo na nova svojstva. U uvodnom predavanju ste saznali da općenito ne smijemo "dijeliti" kongruencije. Na primjer,
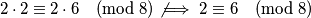
Dakle, u ovom slučaju nismo smijeli podijeliti obje strane sa  . Prvi izraz je točan, a drugi kriv. Razlog iza toga je što je
. Prvi izraz je točan, a drugi kriv. Razlog iza toga je što je 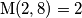 , tj.
, tj.  i
i  nisu relativno prosti brojevi pa općenito ne smijemo dijeliti sa
nisu relativno prosti brojevi pa općenito ne smijemo dijeliti sa  kada radimo modulo
kada radimo modulo  .
.
Kako bismo ovo izrazili malo preciznije, primijetimo da "uvijek smijemo dijeliti s  modulo
modulo  " možemo ekvivalentno zapisati kao "postoji neki
" možemo ekvivalentno zapisati kao "postoji neki 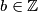 takav da je
takav da je 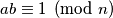 ". Uistinu, onda bismo bilo koju jednadžbu oblika
". Uistinu, onda bismo bilo koju jednadžbu oblika 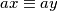 mogli manipulirati ovako
mogli manipulirati ovako
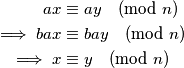
gdje smo od prve do druge crte došli množenjem obje strane sa  (to uvijek smijemo), a od druge od treće koristeći činjenicu da je
(to uvijek smijemo), a od druge od treće koristeći činjenicu da je 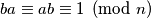 (množenje komutira). Dakle, dobili smo način za dijeliti bez da smo pričali o dijeljenju kao operaciji. Ovo je puno lakše za formalizirati od toga da uvodimo cijelu novu operaciju pa ćemo od sada raditi tako. Broj
(množenje komutira). Dakle, dobili smo način za dijeliti bez da smo pričali o dijeljenju kao operaciji. Ovo je puno lakše za formalizirati od toga da uvodimo cijelu novu operaciju pa ćemo od sada raditi tako. Broj  zovemo multiplikativni inverz od
zovemo multiplikativni inverz od  modulo
modulo  i često pišemo
i često pišemo 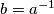 . Primijetite da je sada "očito" zašto ne smijemo dijeliti sa
. Primijetite da je sada "očito" zašto ne smijemo dijeliti sa  modulo
modulo  : da za neki
: da za neki 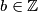 vrijedi
vrijedi 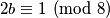 , imali bismo
, imali bismo 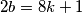 (po definiciji kongruencija) za neki
(po definiciji kongruencija) za neki 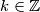 , ali to je nemoguće jer je lijeva strana parna, a desna neparna. Bitno je vidjeti da se to dogodilo upravo zato što
, ali to je nemoguće jer je lijeva strana parna, a desna neparna. Bitno je vidjeti da se to dogodilo upravo zato što  i
i  imaju najveći zajednički djelitelj različit od
imaju najveći zajednički djelitelj različit od  .
.
U idućoj sekciji ćemo dati neke rezultate o tome kad postoje multiplikativni inverzi.
Upišite 1 za nastavak.
Dobrodošli u 6. tjedan tečaja. Tema ovog tjedna su kongruencije i njihova svojstva, tj. područje kojim se bavimo je teorija brojeva. Ako čitate ove primjere, nadam se da ste već pogledali uvodno predavanje profesorice Zelčić. Ovdje ćemo samo proći neka dodatna svojstva kongruencija te par primjera. Ako želite pogledati nešto o osnovnim svojstvima u tekstualnom obliku, preporučujem \href{https://mnm.hr/wp-content/uploads/2015/10/kongruencije.pdf}{ovaj dokument.}
Sada pređimo na nova svojstva. U uvodnom predavanju ste saznali da općenito \textbf{ne} smijemo "dijeliti" kongruencije. Na primjer,
$$2 \cdot 2 \equiv 2 \cdot 6 \pmod{8} \not\implies 2 \equiv 6 \pmod{8}$$
Dakle, u ovom slučaju nismo smijeli podijeliti obje strane sa $2$. Prvi izraz je točan, a drugi kriv. Razlog iza toga je što je $\mathrm{M}(2, 8) = 2$, tj. $2$ i $8$ nisu relativno prosti brojevi pa općenito ne smijemo dijeliti sa $2$ kada radimo modulo $8$.
Kako bismo ovo izrazili malo preciznije, primijetimo da "uvijek smijemo dijeliti s $a$ modulo $n$" možemo ekvivalentno zapisati kao "postoji neki $b \in \mathbb{Z}$ takav da je $ab \equiv 1 \pmod{n}$". Uistinu, onda bismo bilo koju jednadžbu oblika $ax \equiv ay$ mogli manipulirati ovako
\begin{equation}
\notag
\begin{split}
ax &\equiv ay \pmod{n} \\
\implies bax &\equiv bay \pmod{n} \\
\implies x &\equiv y \pmod{n}
\end{split}
\end{equation}
gdje smo od prve do druge crte došli množenjem obje strane sa $b$ (to uvijek smijemo), a od druge od treće koristeći činjenicu da je $ba \equiv ab \equiv 1 \pmod{n}$ (množenje komutira). Dakle, dobili smo način za dijeliti bez da smo pričali o dijeljenju kao operaciji. Ovo je puno lakše za formalizirati od toga da uvodimo cijelu novu operaciju pa ćemo od sada raditi tako. Broj $b$ zovemo \textit{multiplikativni inverz od $a$ modulo $n$} i često pišemo $b = a^{-1}$. Primijetite da je sada "očito" zašto ne smijemo dijeliti sa $2$ modulo $8$: da za neki $b \in \mathbb{Z}$ vrijedi $2b \equiv 1 \pmod{8}$, imali bismo $2b = 8k + 1$ (po definiciji kongruencija) za neki $k \in \mathbb{Z}$, ali to je nemoguće jer je lijeva strana parna, a desna neparna. Bitno je vidjeti da se to dogodilo upravo zato što $2$ i $8$ imaju najveći zajednički djelitelj različit od $1$.
U idućoj sekciji ćemo dati neke rezultate o tome kad postoje multiplikativni inverzi.
Upišite 1 za nastavak.
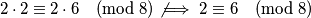
 . Prvi izraz je točan, a drugi kriv. Razlog iza toga je što je
. Prvi izraz je točan, a drugi kriv. Razlog iza toga je što je 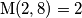 , tj.
, tj.  i
i  nisu relativno prosti brojevi pa općenito ne smijemo dijeliti sa
nisu relativno prosti brojevi pa općenito ne smijemo dijeliti sa  kada radimo modulo
kada radimo modulo  .
. modulo
modulo  " možemo ekvivalentno zapisati kao "postoji neki
" možemo ekvivalentno zapisati kao "postoji neki 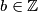 takav da je
takav da je 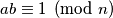 ". Uistinu, onda bismo bilo koju jednadžbu oblika
". Uistinu, onda bismo bilo koju jednadžbu oblika 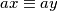 mogli manipulirati ovako
mogli manipulirati ovako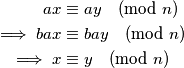
 (to uvijek smijemo), a od druge od treće koristeći činjenicu da je
(to uvijek smijemo), a od druge od treće koristeći činjenicu da je 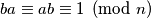 (množenje komutira). Dakle, dobili smo način za dijeliti bez da smo pričali o dijeljenju kao operaciji. Ovo je puno lakše za formalizirati od toga da uvodimo cijelu novu operaciju pa ćemo od sada raditi tako. Broj
(množenje komutira). Dakle, dobili smo način za dijeliti bez da smo pričali o dijeljenju kao operaciji. Ovo je puno lakše za formalizirati od toga da uvodimo cijelu novu operaciju pa ćemo od sada raditi tako. Broj  zovemo multiplikativni inverz od
zovemo multiplikativni inverz od  modulo
modulo  i često pišemo
i često pišemo 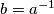 . Primijetite da je sada "očito" zašto ne smijemo dijeliti sa
. Primijetite da je sada "očito" zašto ne smijemo dijeliti sa  modulo
modulo  : da za neki
: da za neki 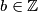 vrijedi
vrijedi 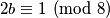 , imali bismo
, imali bismo 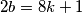 (po definiciji kongruencija) za neki
(po definiciji kongruencija) za neki 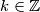 , ali to je nemoguće jer je lijeva strana parna, a desna neparna. Bitno je vidjeti da se to dogodilo upravo zato što
, ali to je nemoguće jer je lijeva strana parna, a desna neparna. Bitno je vidjeti da se to dogodilo upravo zato što  i
i  imaju najveći zajednički djelitelj različit od
imaju najveći zajednički djelitelj različit od  .
.