Kongruencije i multiplikativni inverzi - Primjer 2
Sljedeći teorem kaže kada postoje multiplikativni inverzi u općenitom slučaju.
Teorem 1. Za  i
i 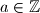 postoji multiplikativni inverz od
postoji multiplikativni inverz od  modulo
modulo  ako i samo ako je
ako i samo ako je 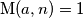 , tj.
, tj.  i
i  su relativno prosti.
su relativno prosti.
Jedan smjer ovog teorema smo praktički već dokazali u prethodnom dijelu uvoda kad smo promatrali primjer o dijeljenju sa  modulo
modulo  . Dokaz u općenitom slučaju je jako sličan, možete pokušati sami ga raspisati.
. Dokaz u općenitom slučaju je jako sličan, možete pokušati sami ga raspisati.
Dokaz drugog smjera nije nešto prosvjetljujuć pa njega nećemo raspisivati. Najbliže tome što je nama korisno je da nam teorem potvrđuje intuiciju iz prethodnog primjera, tj. da multiplikativni inverzi ne postoje točno kad brojevi dijele neki faktor.
Na natjecanju se slobodno smijete pozvati na gornji teorem bez dokaza. Sada primijetimo jedan bitni korolar.
Korolar 1. Za prost  i
i 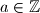 postoji multiplikativni inverz od
postoji multiplikativni inverz od  modulo
modulo  ako i samo ako
ako i samo ako 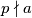 .
.
Dakle, u slučaju kad nešto gledamo modulo  smijemo dijeliti "praktički uvijek", tj. ne smijemo samo u najočitijem slučaju kad dijelimo s nulom.
smijemo dijeliti "praktički uvijek", tj. ne smijemo samo u najočitijem slučaju kad dijelimo s nulom.
Pronaći multiplikativni inverz nekog specifičnog broja modulo nekog drugog specifičnog broja općenito nije lagano. Ako vam to bude potrebno u nekom trenutku, najbolje je samo provjeriti redom sve brojeve dok ne nađete nekog koji radi, ali za druge zadatke je bitno da nemate jednostavnu formulu koja bi vam dala inverz, samo znate da postoji.
Upišite 1 za nastavak.
