Sada ćemo spomenuti jedan jako bitan i koristan teorem.
Teorem 2. (mali Fermatov teorem) Neka je  prost i
prost i 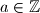 . Vrijedi
. Vrijedi 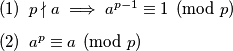
Primijetimo da tvrdnja  zapravo lagano slijedi iz
zapravo lagano slijedi iz  množenjem obje strane s
množenjem obje strane s  ako
ako 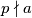 . U drugom slučaju je zapravo još lakše, jer je očito
. U drugom slučaju je zapravo još lakše, jer je očito 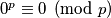 . Uglavnom zato koristimo
. Uglavnom zato koristimo  , ali
, ali  je ponekad korisna jer ne trebamo pretpostavku da
je ponekad korisna jer ne trebamo pretpostavku da 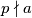 . Sada ćemo dokazati
. Sada ćemo dokazati  .
.
Dokaz.
Neka je  prost i
prost i  takav da
takav da 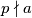 . Promotrimo skupove
. Promotrimo skupove 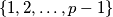 i
i 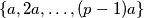 . Tvrdimo da, iako ne nužno u istom poretku, oni daju iste ostatke modulo
. Tvrdimo da, iako ne nužno u istom poretku, oni daju iste ostatke modulo  . Na primjer, postoji neki
. Na primjer, postoji neki 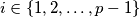 takav da je
takav da je 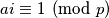 , postoji neki
, postoji neki  takav da je
takav da je 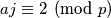 , itd. Dokaz nije težak, ali je dobra vježba pa je ostavljen vama u sklopu Zadatka 3 iz lakšeg lanca.
, itd. Dokaz nije težak, ali je dobra vježba pa je ostavljen vama u sklopu Zadatka 3 iz lakšeg lanca.
Dakle, znamo da ti skupovi daju iste ostatke, tj. oni su "isti" modulo  . To znači da ako napravimo neku operaciju na prvom skupu, ona mora dati isti rezultat (modulo
. To znači da ako napravimo neku operaciju na prvom skupu, ona mora dati isti rezultat (modulo  ) kad je napravimo na drugom skupu. Posebno, umnožak svih elemenata iz prvog skupa kongruentan je umnošku svih elemenata iz drugog skupa, tj.
) kad je napravimo na drugom skupu. Posebno, umnožak svih elemenata iz prvog skupa kongruentan je umnošku svih elemenata iz drugog skupa, tj.
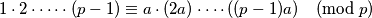
To možemo zapisati i kao
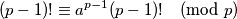
Primijetite da bismo dobili što želimo da možemo pokratiti 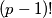 pa ostaje to opravdati. To smijemo po Korolaru 1. akko
pa ostaje to opravdati. To smijemo po Korolaru 1. akko 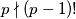 . Da
. Da 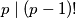 , onda bi
, onda bi  nužno dijelio neki od faktora (to je poznato svojstvo prostih brojeva), tj.
nužno dijelio neki od faktora (to je poznato svojstvo prostih brojeva), tj. 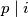 za neki
za neki 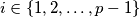 . Međutim,
. Međutim, 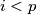 pa je to nemoguće i imamo kontradikciju. Zaključujemo da postoji inverz od
pa je to nemoguće i imamo kontradikciju. Zaključujemo da postoji inverz od 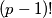 pa imamo
pa imamo
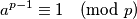
što smo i htjeli dokazati.
Kao napomenu koja se nadovezuje na ono što smo prije komentirali, primijetite da vam gornji teorem daje način za "eksplicitno" odrediti modularni inverz od  modulo
modulo  --- to je samo
--- to je samo 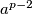 (pomnožite ih ako vam nije očito). Ovo je ponekad korisna činjenica u zadatcima gdje
(pomnožite ih ako vam nije očito). Ovo je ponekad korisna činjenica u zadatcima gdje  i
i  nisu zadani kao konkretni brojevi --- ako su vam zadani konkretni brojevi, ovo nije nešto brže od jednostavne provjere svih mogućnosti za inverz od
nisu zadani kao konkretni brojevi --- ako su vam zadani konkretni brojevi, ovo nije nešto brže od jednostavne provjere svih mogućnosti za inverz od  .
.
Upišite 1 za nastavak.
Sada ćemo spomenuti jedan jako bitan i koristan teorem.
\textbf{Teorem 2. (mali Fermatov teorem)} Neka je $p$ prost i $a \in \mathbb{Z}$. Vrijedi
\begin{enumerate}
\renewcommand{\labelenumi}{(\arabic{enumi})}
\item $p \nmid a \implies a^{p - 1} \equiv 1 \pmod{p}$
\item $a^p \equiv a \pmod{p}$
\end{enumerate}
Primijetimo da tvrdnja $(2)$ zapravo lagano slijedi iz $(1)$ množenjem obje strane s $a$ ako $p \nmid a$. U drugom slučaju je zapravo još lakše, jer je očito $0^p \equiv 0 \pmod{p}$. Uglavnom zato koristimo $(1)$, ali $(2)$ je ponekad korisna jer ne trebamo pretpostavku da $p \nmid a$. Sada ćemo dokazati $(1)$.
\textbf{Dokaz.}
Neka je $p$ prost i $a$ takav da $p \nmid a$. Promotrimo skupove $\{1, 2, \dots, p - 1\}$ i $\{a, 2a, \dots, (p - 1)a\}$. Tvrdimo da, iako ne nužno u istom poretku, oni daju iste ostatke modulo $p$. Na primjer, postoji neki $i \in \{1, 2, \dots, p - 1\}$ takav da je $ai \equiv 1 \pmod{p}$, postoji neki $j$ takav da je $aj \equiv 2 \pmod{p}$, itd. Dokaz nije težak, ali je dobra vježba pa je ostavljen vama u sklopu Zadatka 3 iz lakšeg lanca.
Dakle, znamo da ti skupovi daju iste ostatke, tj. oni su "isti" modulo $p$. To znači da ako napravimo neku operaciju na prvom skupu, ona mora dati isti rezultat (modulo $p$) kad je napravimo na drugom skupu. Posebno, umnožak svih elemenata iz prvog skupa kongruentan je umnošku svih elemenata iz drugog skupa, tj.
$$1 \cdot 2 \cdot \cdots \cdot (p - 1) \equiv a \cdot (2a) \cdot \cdots ((p - 1)a) \pmod{p}$$
To možemo zapisati i kao
$$(p - 1)! \equiv a^{p - 1} (p - 1)! \pmod{p}$$
Primijetite da bismo dobili što želimo da možemo pokratiti $(p - 1)!$ pa ostaje to opravdati. To smijemo po \textbf{Korolaru 1.} akko $p \nmid (p - 1)!$. Da $p \mid (p - 1)!$, onda bi $p$ nužno dijelio neki od faktora (to je poznato svojstvo prostih brojeva), tj. $p \mid i$ za neki $i \in \{1, 2, \dots, p - 1\}$. Međutim, $i < p$ pa je to nemoguće i imamo kontradikciju. Zaključujemo da postoji inverz od $(p - 1)!$ pa imamo
$$a^{p - 1} \equiv 1 \pmod{p}$$
što smo i htjeli dokazati.
Kao napomenu koja se nadovezuje na ono što smo prije komentirali, primijetite da vam gornji teorem daje način za "eksplicitno" odrediti modularni inverz od $a$ modulo $p$ --- to je samo $a^{p - 2}$ (pomnožite ih ako vam nije očito). Ovo je ponekad korisna činjenica u zadatcima gdje $a$ i $p$ \textit{nisu} zadani kao konkretni brojevi --- ako su vam zadani konkretni brojevi, ovo nije nešto brže od jednostavne provjere svih mogućnosti za inverz od $a$.
Upišite 1 za nastavak.
 prost i
prost i 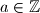 . Vrijedi
. Vrijedi 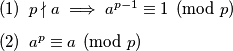
 zapravo lagano slijedi iz
zapravo lagano slijedi iz  množenjem obje strane s
množenjem obje strane s  ako
ako 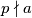 . U drugom slučaju je zapravo još lakše, jer je očito
. U drugom slučaju je zapravo još lakše, jer je očito 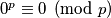 . Uglavnom zato koristimo
. Uglavnom zato koristimo  , ali
, ali  je ponekad korisna jer ne trebamo pretpostavku da
je ponekad korisna jer ne trebamo pretpostavku da 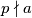 . Sada ćemo dokazati
. Sada ćemo dokazati  .
. prost i
prost i  takav da
takav da 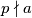 . Promotrimo skupove
. Promotrimo skupove 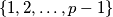 i
i 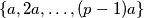 . Tvrdimo da, iako ne nužno u istom poretku, oni daju iste ostatke modulo
. Tvrdimo da, iako ne nužno u istom poretku, oni daju iste ostatke modulo  . Na primjer, postoji neki
. Na primjer, postoji neki 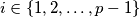 takav da je
takav da je 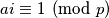 , postoji neki
, postoji neki  takav da je
takav da je 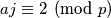 , itd. Dokaz nije težak, ali je dobra vježba pa je ostavljen vama u sklopu Zadatka 3 iz lakšeg lanca.
, itd. Dokaz nije težak, ali je dobra vježba pa je ostavljen vama u sklopu Zadatka 3 iz lakšeg lanca. . To znači da ako napravimo neku operaciju na prvom skupu, ona mora dati isti rezultat (modulo
. To znači da ako napravimo neku operaciju na prvom skupu, ona mora dati isti rezultat (modulo  ) kad je napravimo na drugom skupu. Posebno, umnožak svih elemenata iz prvog skupa kongruentan je umnošku svih elemenata iz drugog skupa, tj.
) kad je napravimo na drugom skupu. Posebno, umnožak svih elemenata iz prvog skupa kongruentan je umnošku svih elemenata iz drugog skupa, tj.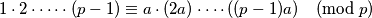
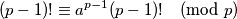
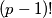 pa ostaje to opravdati. To smijemo po Korolaru 1. akko
pa ostaje to opravdati. To smijemo po Korolaru 1. akko 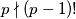 . Da
. Da 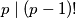 , onda bi
, onda bi  nužno dijelio neki od faktora (to je poznato svojstvo prostih brojeva), tj.
nužno dijelio neki od faktora (to je poznato svojstvo prostih brojeva), tj. 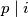 za neki
za neki 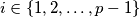 . Međutim,
. Međutim, 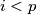 pa je to nemoguće i imamo kontradikciju. Zaključujemo da postoji inverz od
pa je to nemoguće i imamo kontradikciju. Zaključujemo da postoji inverz od 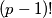 pa imamo
pa imamo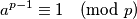
 modulo
modulo  --- to je samo
--- to je samo 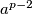 (pomnožite ih ako vam nije očito). Ovo je ponekad korisna činjenica u zadatcima gdje
(pomnožite ih ako vam nije očito). Ovo je ponekad korisna činjenica u zadatcima gdje  i
i  nisu zadani kao konkretni brojevi --- ako su vam zadani konkretni brojevi, ovo nije nešto brže od jednostavne provjere svih mogućnosti za inverz od
nisu zadani kao konkretni brojevi --- ako su vam zadani konkretni brojevi, ovo nije nešto brže od jednostavne provjere svih mogućnosti za inverz od  .
.