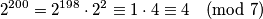Sada je dobro vrijeme za jednostavnu primjenu kongruencija.
Primjer 1. Odredite ostatak od  pri dijeljenju sa
pri dijeljenju sa  .
.
Postoje dva načina. Prvi je da promotrimo prvih par potencija od  modulo
modulo  . Imamo
. Imamo
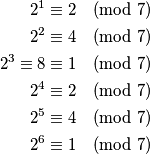
Primijetite da, kad računate ostatak od npr.  , nema potrebe računati da je
, nema potrebe računati da je 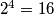 pa onda tražiti ostatak. Možete samo koristiti činjenicu da kongruencije smijemo množiti i iskoristiti to da iz prethodnog koraka znamo da je
pa onda tražiti ostatak. Možete samo koristiti činjenicu da kongruencije smijemo množiti i iskoristiti to da iz prethodnog koraka znamo da je  . Onda je
. Onda je
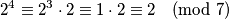
što nam dosta olakšava, a olaškavalo bi i više da su brojevi nešto veći. Ali primijetite da onda znamo da iduća potencija ovisi samo o trenutnoj, pa ako je npr 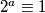 za neki
za neki  i
i 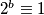 za neki
za neki  , imat ćemo
, imat ćemo 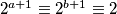 , tj. iduća potencija ne ovisi uopće o tim
, tj. iduća potencija ne ovisi uopće o tim  i
i  , već samo o toj trenutnoj potenciji. Onda možemo iz gornjeg zaključiti da će se potencije ponavljati ciklično nakon
, već samo o toj trenutnoj potenciji. Onda možemo iz gornjeg zaključiti da će se potencije ponavljati ciklično nakon 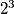 (gore su zapravo raspisana prva dva ciklusa) i to s periodom
(gore su zapravo raspisana prva dva ciklusa) i to s periodom  . Dakle,
. Dakle, 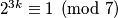 za sve
za sve  . Onda je, zbog
. Onda je, zbog  ,
,
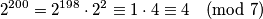
Upišite 1 za nastavak.
Sada je dobro vrijeme za jednostavnu primjenu kongruencija.
\textbf{Primjer 1.} Odredite ostatak od $2^{200}$ pri dijeljenju sa $7$.
Postoje dva načina. Prvi je da promotrimo prvih par potencija od $2$ modulo $7$. Imamo
\begin{equation}
\notag
\begin{split}
2^1 &\equiv 2 \pmod{7} \\
2^2 &\equiv 4 \pmod{7} \\
2^3 \equiv 8 &\equiv 1 \pmod {7} \\
2^4 &\equiv 2 \pmod{7} \\
2^5 &\equiv 4 \pmod{7} \\
2^6 &\equiv 1 \pmod{7}
\end{split}
\end{equation}
Primijetite da, kad računate ostatak od npr. $2^4$, nema potrebe računati da je $2^4 = 16$ pa onda tražiti ostatak. Možete samo koristiti činjenicu da kongruencije smijemo množiti i iskoristiti to da iz prethodnog koraka znamo da je $2^3 \equiv 1 \pmod{7}$. Onda je
$$2^4 \equiv 2^3 \cdot 2 \equiv 1 \cdot 2 \equiv 2 \pmod{7}$$
što nam dosta olakšava, a olaškavalo bi i više da su brojevi nešto veći. Ali primijetite da onda znamo da iduća potencija ovisi samo o trenutnoj, pa ako je npr $2^a \equiv 1$ za neki $a$ i $2^b \equiv 1$ za neki $b$, imat ćemo $2^{a + 1} \equiv 2^{b + 1} \equiv 2$, tj. iduća potencija ne ovisi uopće o tim $a$ i $b$, već samo o toj trenutnoj potenciji. Onda možemo iz gornjeg zaključiti da će se potencije ponavljati ciklično nakon $2^3$ (gore su zapravo raspisana prva dva ciklusa) i to s periodom $3$. Dakle, $2^{3k} \equiv 1 \pmod{7}$ za sve $k \in \mathbb{N}$. Onda je, zbog $200 = 198 + 2$,
$$2^{200} = 2^{198} \cdot 2^2 \equiv 1 \cdot 4 \equiv 4 \pmod{7}$$
Upišite 1 za nastavak.
 pri dijeljenju sa
pri dijeljenju sa  .
. modulo
modulo  . Imamo
. Imamo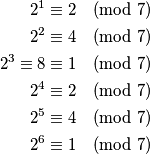
 , nema potrebe računati da je
, nema potrebe računati da je 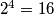 pa onda tražiti ostatak. Možete samo koristiti činjenicu da kongruencije smijemo množiti i iskoristiti to da iz prethodnog koraka znamo da je
pa onda tražiti ostatak. Možete samo koristiti činjenicu da kongruencije smijemo množiti i iskoristiti to da iz prethodnog koraka znamo da je  . Onda je
. Onda je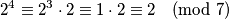
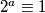 za neki
za neki  i
i 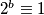 za neki
za neki  , imat ćemo
, imat ćemo 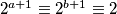 , tj. iduća potencija ne ovisi uopće o tim
, tj. iduća potencija ne ovisi uopće o tim  i
i  , već samo o toj trenutnoj potenciji. Onda možemo iz gornjeg zaključiti da će se potencije ponavljati ciklično nakon
, već samo o toj trenutnoj potenciji. Onda možemo iz gornjeg zaključiti da će se potencije ponavljati ciklično nakon 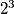 (gore su zapravo raspisana prva dva ciklusa) i to s periodom
(gore su zapravo raspisana prva dva ciklusa) i to s periodom  . Dakle,
. Dakle, 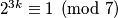 za sve
za sve  . Onda je, zbog
. Onda je, zbog  ,
,