Sada ćemo proći još jednu korisnu primjenu kongruencija.
Primjer 2. Odredite sve prirodne brojeve 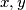 takve da je
takve da je  .
.
Promotrimo koje sve ostatke kvadrati mogu davati pri dijeljenju sa  . Neka je
. Neka je  neki prirodan broj. Koristeći činjenicu da kongruencije smijemo množiti (a time i kvadrirati), imamo
neki prirodan broj. Koristeći činjenicu da kongruencije smijemo množiti (a time i kvadrirati), imamo

Dakle, za sve  ,
,  ili
ili  modulo
modulo  . Reduciramo jednadžbu modulo
. Reduciramo jednadžbu modulo  i rješavamo slučajeve. Imamo
i rješavamo slučajeve. Imamo

Prvi slučaj je  ,
,  , ali onda je
, ali onda je  .
.
Drugi slučaj je  ,
,  , ali onda je
, ali onda je  .
.
Druga dva slučaja možete provjeriti sami, ali vidjet ćete da opet imamo kontradikciju s početnom jednadžbom. Dakle, jednadžba nema rješenja.
Kako bismo se sjetili promatrati gornju jednadžbu modulo  ? Jednostavan odgovor je da je ovo jako česta ideja (to jest: ne bismo se sjetili ako to već nismo vidjeli). Općenito će kvadrati (i druge potencije) davati samo neke ostatke modulo
? Jednostavan odgovor je da je ovo jako česta ideja (to jest: ne bismo se sjetili ako to već nismo vidjeli). Općenito će kvadrati (i druge potencije) davati samo neke ostatke modulo  pa to često može eliminirati puno mogućih vrijednosti metodama sličnim ovoj gore. Drugi brojevi koji najčešće rade za
pa to često može eliminirati puno mogućih vrijednosti metodama sličnim ovoj gore. Drugi brojevi koji najčešće rade za  su
su  i
i  , ali u principu bilo koji broj može biti koristan ovisno o zadatku.
, ali u principu bilo koji broj može biti koristan ovisno o zadatku.
Upišite 1 za završetak.
Sada ćemo proći još jednu korisnu primjenu kongruencija.
\textbf{Primjer 2.} Odredite sve prirodne brojeve $x, y$ takve da je $x^2 + y^2 = 2023$.
Promotrimo koje sve ostatke kvadrati mogu davati pri dijeljenju sa $4$. Neka je $x$ neki prirodan broj. Koristeći činjenicu da kongruencije smijemo množiti (a time i kvadrirati), imamo
\begin{equation}
\notag
\begin{split}
x \equiv 0 \pmod{4} &\implies x^2 \equiv 0 \pmod{4} \\
x \equiv 1 \pmod{4} &\implies x^2 \equiv 1 \pmod{4} \\
x \equiv 2 \pmod{4} &\implies x^2 \equiv 4 \equiv 0 \pmod{4} \\
x \equiv 3 \pmod{4} &\implies x^2 \equiv 9 \equiv 1 \pmod{4} \\
\end{split}
\end{equation}
Dakle, za sve $x$, $x^2 \equiv 0$ ili $x^2 \equiv 1$ modulo $4$. Reduciramo jednadžbu modulo $4$ i rješavamo slučajeve. Imamo
$$x^2 + y^2 \equiv 3 \pmod{4}$$
Prvi slučaj je $x^2 \equiv 0$, $y^2 \equiv 0$, ali onda je $x^2 + y^2 \equiv 0 \not\equiv 3 \pmod{4}$.
Drugi slučaj je $x^2 \equiv 1$, $y^2 \equiv 0$, ali onda je $x^2 + y^2 \equiv 1 \not\equiv 3 \pmod{4}$.
Druga dva slučaja možete provjeriti sami, ali vidjet ćete da opet imamo kontradikciju s početnom jednadžbom. Dakle, jednadžba nema rješenja.
Kako bismo se sjetili promatrati gornju jednadžbu modulo $4$? Jednostavan odgovor je da je ovo jako česta ideja (to jest: ne bismo se sjetili ako to već nismo vidjeli). Općenito će kvadrati (i druge potencije) davati samo neke ostatke modulo $n$ pa to često može eliminirati puno mogućih vrijednosti metodama sličnim ovoj gore. Drugi brojevi koji najčešće rade za $n$ su $3$ i $8$, ali u principu bilo koji broj može biti koristan ovisno o zadatku.
Upišite 1 za završetak.
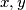 takve da je
takve da je  .
. . Neka je
. Neka je  neki prirodan broj. Koristeći činjenicu da kongruencije smijemo množiti (a time i kvadrirati), imamo
neki prirodan broj. Koristeći činjenicu da kongruencije smijemo množiti (a time i kvadrirati), imamo
 ,
,  ili
ili  modulo
modulo  . Reduciramo jednadžbu modulo
. Reduciramo jednadžbu modulo  i rješavamo slučajeve. Imamo
i rješavamo slučajeve. Imamo
 ,
,  , ali onda je
, ali onda je  .
. ,
,  , ali onda je
, ali onda je  .
. ? Jednostavan odgovor je da je ovo jako česta ideja (to jest: ne bismo se sjetili ako to već nismo vidjeli). Općenito će kvadrati (i druge potencije) davati samo neke ostatke modulo
? Jednostavan odgovor je da je ovo jako česta ideja (to jest: ne bismo se sjetili ako to već nismo vidjeli). Općenito će kvadrati (i druge potencije) davati samo neke ostatke modulo  pa to često može eliminirati puno mogućih vrijednosti metodama sličnim ovoj gore. Drugi brojevi koji najčešće rade za
pa to često može eliminirati puno mogućih vrijednosti metodama sličnim ovoj gore. Drugi brojevi koji najčešće rade za  su
su  i
i  , ali u principu bilo koji broj može biti koristan ovisno o zadatku.
, ali u principu bilo koji broj može biti koristan ovisno o zadatku.