Ortocentar
Definicija
Ortocentar trokuta je sjecište triju pravaca na kojima leže visine trokuta.
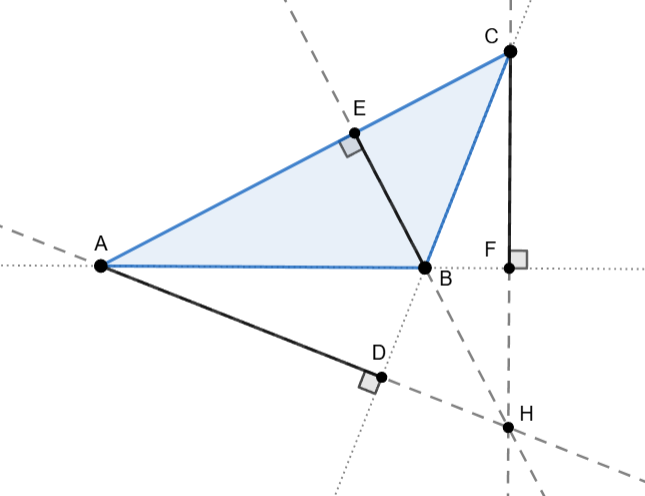
Uočite da nismo ortocentar definirali kao "sjecište visina trokuta". To je zbog toga što se same visine ne moraju uopće sijeći! Takav je primjerice ovaj trokut:
U ovom trokutu ortocentar nije unutar trokuta. U šiljastokutnim trokutima ortocentar će biti unutar trokuta. Ortocentar trokuta najčešće označavamo slovom  .
.
Dokaz da se sva ta tri pravca koji sadrže visine sijeku u jednoj točki možete vidjeti ovdje.
Sljedeći primjer jedan je od najvjerojatnijih zadataka s kojima se možete susresti ako rješavate zadatke s ortocentrom.
Primjer
Neka je  ortocentar trokuta
ortocentar trokuta 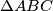 . Dokažite da osnosimetrične slike točke
. Dokažite da osnosimetrične slike točke  s obzirom na stranice trokuta leže na opisanoj kružnici tog trokuta.
s obzirom na stranice trokuta leže na opisanoj kružnici tog trokuta.
Rješenje:
Prvo se moramo podsjetiti što je osnosimetrična slika točke s obzirom na neku dužinu. Općenito, osnosimetrična slika točke  s obzirom na dužinu
s obzirom na dužinu  (ili pravac
(ili pravac  ) je točka
) je točka 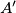 takva da je
takva da je  simetrala dužine
simetrala dužine 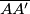 . To zapravo znači da
. To zapravo znači da 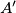 leži na pravcu koji sadrži okomicu iz
leži na pravcu koji sadrži okomicu iz  na
na  i jednako je udaljena od
i jednako je udaljena od  kao i
kao i  .
.
Vratimo se sada na zadatak. Neka je točka  osnosimetrična slika točke ortocentra
osnosimetrična slika točke ortocentra  s obzirom na stranicu
s obzirom na stranicu  . Ako pokažemo da je četverokut
. Ako pokažemo da je četverokut 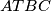 tetivan, pokazat ćemo zapravo da
tetivan, pokazat ćemo zapravo da  leži na kružnici opisanoj trokutu
leži na kružnici opisanoj trokutu  .
.
Označimo s  ,
,  i
i  redom nožišta visina iz
redom nožišta visina iz  ,
,  i
i  te kut
te kut 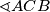 s
s  .
.
Budući da je kut 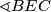 pravi, u četverokutu
pravi, u četverokutu 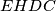 imamo dva nasuprotna kuta prava pa on mora biti tetivan! Zato i zbroj preostala dva kuta mora biti jednak
imamo dva nasuprotna kuta prava pa on mora biti tetivan! Zato i zbroj preostala dva kuta mora biti jednak 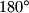 pa je
pa je 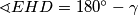 . Sada možemo uočiti neke vršne kuteve:
. Sada možemo uočiti neke vršne kuteve:  .
.
Što još uopće nismo iskoristili?  je osnosimetrična slika točke
je osnosimetrična slika točke  u odnosu na
u odnosu na  pa mora vrijediti
pa mora vrijediti 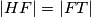 ,
, 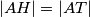 i
i 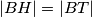 . No, sada vidimo i sukladne trokute
. No, sada vidimo i sukladne trokute 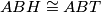 (sukladni su po poučku SSS) pa znamo da su im i kutevi jednaki. Dakle,
(sukladni su po poučku SSS) pa znamo da su im i kutevi jednaki. Dakle, 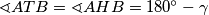 .
.
Zapravo smo gotovi! Dobili smo sljedeće: 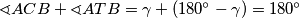 , a četverokut koji ima nasuprotne kuteve koji u zbroju daju
, a četverokut koji ima nasuprotne kuteve koji u zbroju daju 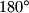 mora biti tetivan.
mora biti tetivan.
Naravno, na isti način sada bismo mogli pokazati i da osnosimetrične slike ortocentra s obzirom na preostale stranice također leže na opisanoj kružnici, odnosno čine odgovarajući tetivni četverokut.
Ovaj primjer možda izgleda malo zastrašujuće i dugačko. Bez brige, nije baš najlakši zadatak ikad. No, u sebi krije jako bitne ideje i objekte -- tetivne četverokute. Jednom kad imamo ortocentar, automatski imamo i  tetivna četverokuta jer imamo puno pravih kuteva, a ako u četverokutu imamo nasuprotne kuteve prave, on mora biti tetivan. To nam je korisno jer tada znamo da i zbroj preostala dva kuta također mora biti
tetivna četverokuta jer imamo puno pravih kuteva, a ako u četverokutu imamo nasuprotne kuteve prave, on mora biti tetivan. To nam je korisno jer tada znamo da i zbroj preostala dva kuta također mora biti 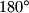 . Na skici u prethodnom primjeru ti tetivni četverokuti su
. Na skici u prethodnom primjeru ti tetivni četverokuti su 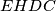 ,
, 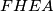 i
i 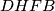 .
.
Za bod upišite kako najčešće označavamo ortocentar trokuta.
\textbf{Ortocentar}
\textbf{Definicija}\\
Ortocentar trokuta je sjecište triju pravaca na kojima leže visine trokuta.
\begin{center}
\includegraphics[scale=0.4]{ortocentar.png}
\end{center}
Uočite da nismo ortocentar definirali kao "sjecište visina trokuta". To je zbog toga što se same visine ne moraju uopće sijeći! Takav je primjerice ovaj trokut:
\begin{center}
\includegraphics[scale=0.4]{tupokutni.png}
\end{center}
U ovom trokutu ortocentar nije unutar trokuta. U šiljastokutnim trokutima ortocentar će biti unutar trokuta.
Ortocentar trokuta najčešće označavamo slovom $H$.
Dokaz da se sva ta tri pravca koji sadrže visine sijeku u jednoj točki možete vidjeti \href{https://artofproblemsolving.com/wiki/index.php/Orthocenter}{ovdje}.
Sljedeći primjer jedan je od najvjerojatnijih zadataka s kojima se možete susresti ako rješavate zadatke s ortocentrom.
\textbf{Primjer}\\
Neka je $H$ ortocentar trokuta $\Delta ABC$. Dokažite da osnosimetrične slike točke $H$ s obzirom na stranice trokuta leže na opisanoj kružnici tog trokuta.
\textit{Rješenje:}\\
Prvo se moramo podsjetiti što je osnosimetrična slika točke s obzirom na neku dužinu. Općenito, osnosimetrična slika točke $A$ s obzirom na dužinu $\overline{BC}$ (ili pravac $BC$) je točka $A'$ takva da je $BC$ simetrala dužine $\overline{AA'}$. To zapravo znači da $A'$ leži na pravcu koji sadrži okomicu iz $A$ na $BC$ i jednako je udaljena od $BC$ kao i $A$.
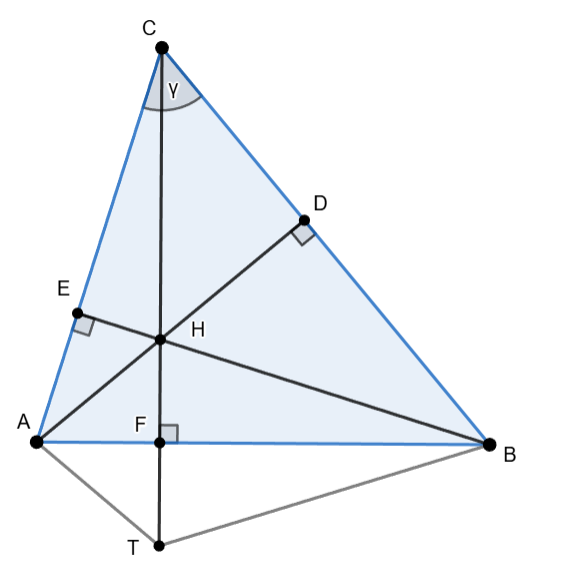
Vratimo se sada na zadatak. Neka je točka $T$ osnosimetrična slika točke ortocentra $H$ s obzirom na stranicu $\overline{AB}$. Ako pokažemo da je četverokut $ATBC$ tetivan, pokazat ćemo zapravo da $T$ leži na kružnici opisanoj trokutu $ABC$.
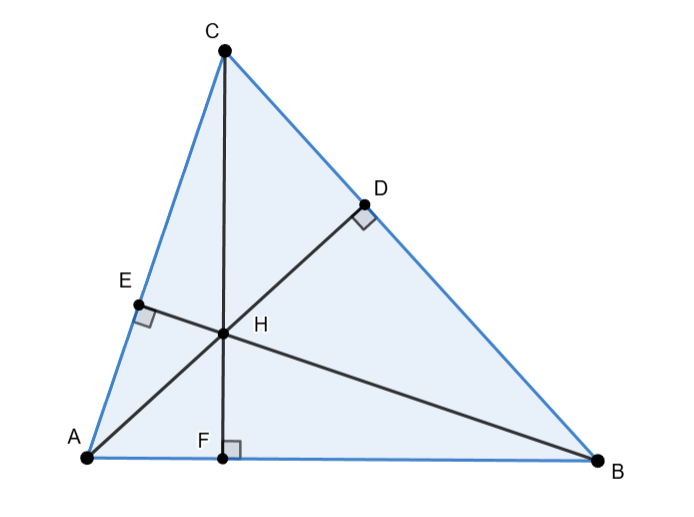
Označimo s $E$, $F$ i $G$ redom nožišta visina iz $A$, $B$ i $C$ te kut $\sphericalangle ACB$ s $\gamma$.
\begin{center}
\includegraphics[scale=0.4]{pr_ort.png}
\end{center}
Budući da je kut $\sphericalangle BEC$ pravi, u četverokutu $EHDC$ imamo dva nasuprotna kuta prava pa on mora biti tetivan! Zato i zbroj preostala dva kuta mora biti jednak $180^\circ$ pa je $\sphericalangle EHD = 180^\circ -\gamma$. Sada možemo uočiti neke vršne kuteve: $\sphericalangle EHD = \sphericalangle AHB = 180^\circ -\gamma$.
Što još uopće nismo iskoristili? $T$ je osnosimetrična slika točke $H$ u odnosu na $\overline{AB}$ pa mora vrijediti $|HF|=|FT|$, $|AH|=|AT|$ i $|BH|=|BT|$. No, sada vidimo i sukladne trokute $ABH\cong ABT$ (sukladni su po poučku SSS) pa znamo da su im i kutevi jednaki. Dakle, $\sphericalangle ATB = \sphericalangle AHB = 180^\circ - \gamma$.
Zapravo smo gotovi! Dobili smo sljedeće: $\sphericalangle ACB + \sphericalangle ATB = \gamma + (180^\circ - \gamma) = 180^\circ$, a četverokut koji ima nasuprotne kuteve koji u zbroju daju $180^\circ$ mora biti tetivan.
Naravno, na isti način sada bismo mogli pokazati i da osnosimetrične slike ortocentra s obzirom na preostale stranice također leže na opisanoj kružnici, odnosno čine odgovarajući tetivni četverokut.
Ovaj primjer možda izgleda malo zastrašujuće i dugačko. Bez brige, nije baš najlakši zadatak ikad. No, u sebi krije jako bitne ideje i objekte -- tetivne četverokute. Jednom kad imamo ortocentar, automatski imamo i $3$ tetivna četverokuta jer imamo puno pravih kuteva, a ako u četverokutu imamo nasuprotne kuteve prave, on mora biti tetivan. To nam je korisno jer tada znamo da i zbroj preostala dva kuta također mora biti $180^\circ$. Na skici u prethodnom primjeru ti tetivni četverokuti su $EHDC$, $FHEA$ i $DHFB$.
Za bod upišite kako najčešće označavamo ortocentar trokuta.
 .
. ortocentar trokuta
ortocentar trokuta 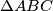 . Dokažite da osnosimetrične slike točke
. Dokažite da osnosimetrične slike točke  s obzirom na stranice trokuta leže na opisanoj kružnici tog trokuta.
s obzirom na stranice trokuta leže na opisanoj kružnici tog trokuta. s obzirom na dužinu
s obzirom na dužinu  (ili pravac
(ili pravac  ) je točka
) je točka 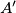 takva da je
takva da je  simetrala dužine
simetrala dužine 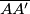 . To zapravo znači da
. To zapravo znači da 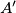 leži na pravcu koji sadrži okomicu iz
leži na pravcu koji sadrži okomicu iz  na
na  i jednako je udaljena od
i jednako je udaljena od  kao i
kao i  .
. osnosimetrična slika točke ortocentra
osnosimetrična slika točke ortocentra  s obzirom na stranicu
s obzirom na stranicu  . Ako pokažemo da je četverokut
. Ako pokažemo da je četverokut 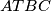 tetivan, pokazat ćemo zapravo da
tetivan, pokazat ćemo zapravo da  leži na kružnici opisanoj trokutu
leži na kružnici opisanoj trokutu  .
. ,
,  i
i  redom nožišta visina iz
redom nožišta visina iz  ,
,  i
i  te kut
te kut 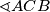 s
s  .
.
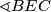 pravi, u četverokutu
pravi, u četverokutu 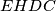 imamo dva nasuprotna kuta prava pa on mora biti tetivan! Zato i zbroj preostala dva kuta mora biti jednak
imamo dva nasuprotna kuta prava pa on mora biti tetivan! Zato i zbroj preostala dva kuta mora biti jednak 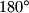 pa je
pa je 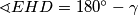 . Sada možemo uočiti neke vršne kuteve:
. Sada možemo uočiti neke vršne kuteve:  .
. je osnosimetrična slika točke
je osnosimetrična slika točke  u odnosu na
u odnosu na  pa mora vrijediti
pa mora vrijediti 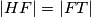 ,
, 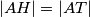 i
i 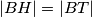 . No, sada vidimo i sukladne trokute
. No, sada vidimo i sukladne trokute 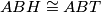 (sukladni su po poučku SSS) pa znamo da su im i kutevi jednaki. Dakle,
(sukladni su po poučku SSS) pa znamo da su im i kutevi jednaki. Dakle, 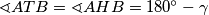 .
.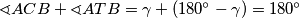 , a četverokut koji ima nasuprotne kuteve koji u zbroju daju
, a četverokut koji ima nasuprotne kuteve koji u zbroju daju 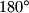 mora biti tetivan.
mora biti tetivan. tetivna četverokuta jer imamo puno pravih kuteva, a ako u četverokutu imamo nasuprotne kuteve prave, on mora biti tetivan. To nam je korisno jer tada znamo da i zbroj preostala dva kuta također mora biti
tetivna četverokuta jer imamo puno pravih kuteva, a ako u četverokutu imamo nasuprotne kuteve prave, on mora biti tetivan. To nam je korisno jer tada znamo da i zbroj preostala dva kuta također mora biti 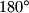 . Na skici u prethodnom primjeru ti tetivni četverokuti su
. Na skici u prethodnom primjeru ti tetivni četverokuti su 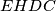 ,
, 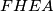 i
i 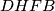 .
.