Karakteristične točke trokuta - središte opisane kružnice
Središte kružnice opisane trokutu
Za sljedeću karakterističnu točku trebat će nam simetrala dužine, pa istaknimo jednu bitnu činjenicu koju znamo o njoj.
Propozicija
Točka  leži na simetrali dužine
leži na simetrali dužine  ako i samo ako je
ako i samo ako je 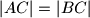 .
.
Primijetite da vrijede obje implikacije, odnosno možemo raditi zaključke u oba smjera. Ako imamo točku na simetrali dužine, ona je jednako udaljena od krajnjih točaka te dužine, ali i ako imamo točku koja je jednako udaljena od krajnjih točaka neke dužine ta točka mora ležati na simetrali te dužine.
Definicija
Središte kružnice opisane trokutu  sjecište je simetrala stranica trokuta
sjecište je simetrala stranica trokuta  .
.
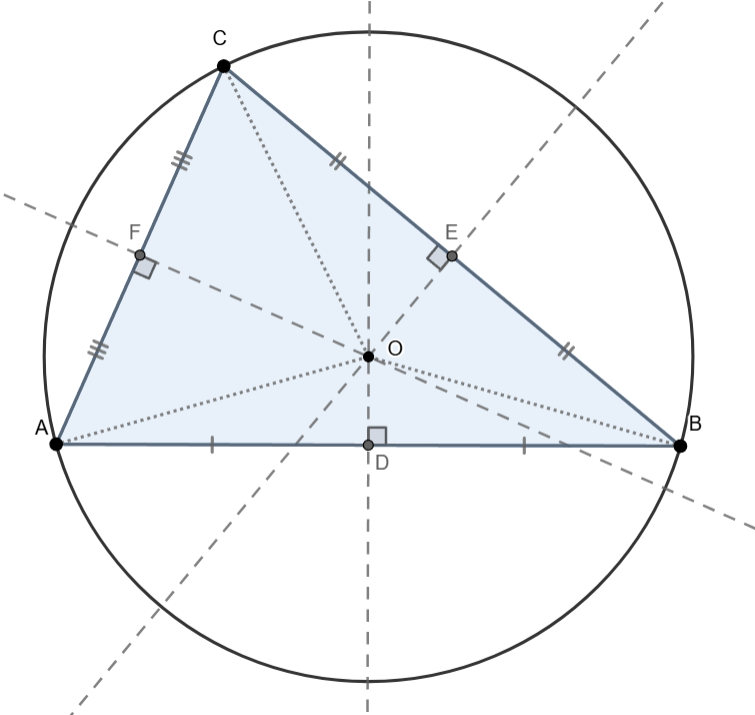
Ponovno ta naša karakteristična točka ne mora biti unutar trokuta.
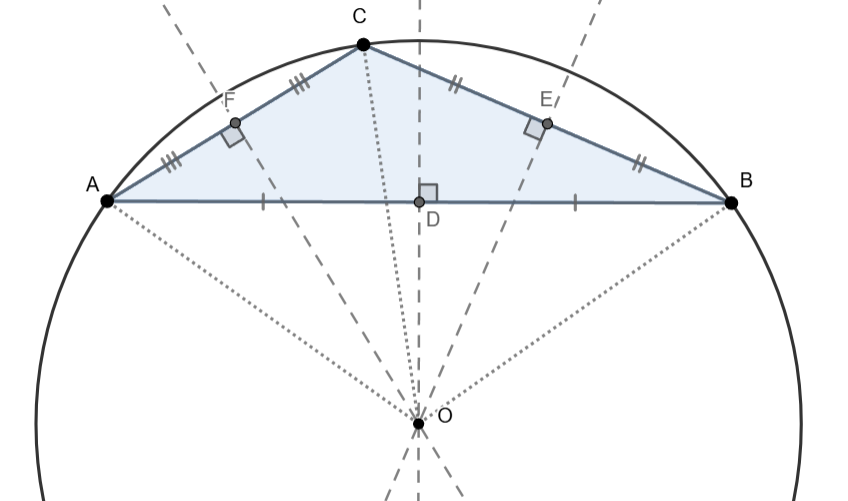
Središte opisane kružnice najčešće označavamo slovom  .
.
Dokaz da se simetrale svih triju stranica trokuta sijeku u jednoj točki možete vidjeti ovdje.
Primijetite da ćemo ponovno imati neke tetivne četverokute. Pokušajte ih pronaći na prethodnim skicama.
Primjer
Dokažite da u šiljastokutnom trokutu  s ortocentrom
s ortocentrom  i središtem opisane kružnice
i središtem opisane kružnice  vrijedi
vrijedi 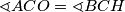 .
.
Rješenje:
Označimo s  nožište visine iz vrha
nožište visine iz vrha  . Uočimo odmah da je kut
. Uočimo odmah da je kut 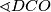 dio oba kuta kojima želimo dokazati jednakost
dio oba kuta kojima želimo dokazati jednakost 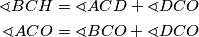 pa nam je dovoljno pokazati da vrijedi
pa nam je dovoljno pokazati da vrijedi 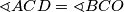 .
.
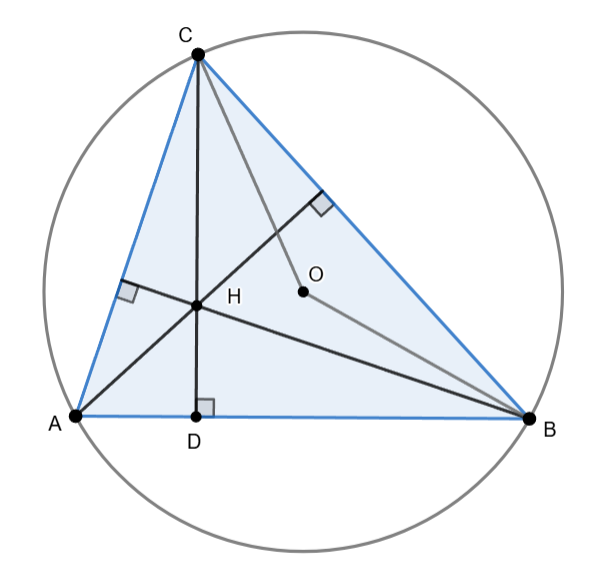
Točka  je središte kružnice opisane trokutu
je središte kružnice opisane trokutu  pa stoga mora biti jednako udaljena od sva tri vrha trokuta. Zato je trokut
pa stoga mora biti jednako udaljena od sva tri vrha trokuta. Zato je trokut 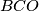 jednakokračan te vrijedi
jednakokračan te vrijedi 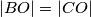 i
i 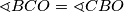 . Također, znamo izračunati i kut
. Također, znamo izračunati i kut 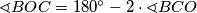 .
.
Sada ćemo ponovno iskoristiti činjenicu da je  središte kružnice na kojoj leže sva tri vrha trokuta. Znamo da je svaki obodni kut upola manji od središnjeg kuta nad istom tetivom. Možemo uočiti da je
središte kružnice na kojoj leže sva tri vrha trokuta. Znamo da je svaki obodni kut upola manji od središnjeg kuta nad istom tetivom. Možemo uočiti da je 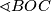 središnji kut obodnog kuta
središnji kut obodnog kuta 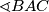 pa zaključujemo da vrijedi
pa zaključujemo da vrijedi 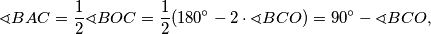 odnosno
odnosno 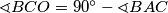 .
.
Konačno, iskoristit ćemo i pretpostavku da je  ortocentar trokuta
ortocentar trokuta  . Konkretno,
. Konkretno,  leži na visini iz vrha
leži na visini iz vrha  i trokut
i trokut 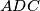 je pravokutan pa vrijedi
je pravokutan pa vrijedi 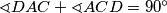 . Dakle,
. Dakle, 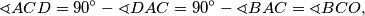 čime smo pokazali našu tvrdnju.
čime smo pokazali našu tvrdnju.
Za bod upišite odgovor na pitanje mora li središte trokutu opisane kružnice uvijek biti unutar trokuta (DA ili NE).
