Središte kružnice upisane trokutu
Za sljedeću karakterističnu točku trebat će nam simetrala kuta, pa istaknimo ponovno jednu bitnu činjenicu.
Propozicija
Točka leži na simetrali kuta ako i samo ako je jednako udaljena od njegovih krakova.
Primijetite da ponovno možemo zaključivati u oba smjera.
Definicija
Središte kružnice upisane trokutu  sjecište je simetrala kuteva trokuta
sjecište je simetrala kuteva trokuta  .
.
Ovaj puta naša karakteristična točka mora biti unutar trokuta neovisno o tome kakav trokut promatramo. Također, ponovno pronalazimo tetivne četverokute: polumjer i tangenta u točki iz koje promatramo polumjer moraju biti okomiti pa ponovno imamo puno pravih kuteva.
Uočimo i da imamo neke jednakosti duljina. Označimo redom s  ,
,  ,
,  točke u kojima upisana kružnica dira stranice
točke u kojima upisana kružnica dira stranice  ,
,  i
i  . Tada po poučku KSK možemo zaključiti da su čak tri para trokuta sukladni:
. Tada po poučku KSK možemo zaključiti da su čak tri para trokuta sukladni:  ,
,  i
i  , odakle zaključujemo i da vrijedi
, odakle zaključujemo i da vrijedi  ,
,  i
i  .
.
Središte upisane kružnice najčešće označavamo slovom  , a dokaz da se simetrale svih triju stranica trokuta sijeku u jednoj točki možete vidjeti ovdje.
, a dokaz da se simetrale svih triju stranica trokuta sijeku u jednoj točki možete vidjeti ovdje.
Primjer
Neka je  trokut za koji vrijedi
trokut za koji vrijedi  . Neka je
. Neka je  sjecište simetrale kuta
sjecište simetrale kuta  sa stranicom
sa stranicom  , a
, a  središte trokutu
središte trokutu  upisane kružnice.
upisane kružnice.
Odredite omjer  .
.
Rješenje:
Označimo  i
i  , te označimo standardno stranice
, te označimo standardno stranice 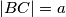 ,
, 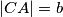 i
i 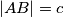 . Uvjet zadatka sada možemo zapisati kao
. Uvjet zadatka sada možemo zapisati kao  , a znamo i da vrijedi
, a znamo i da vrijedi  .
.
Prisjetimo se, simetrala unutarnjeg kuta trokuta dijeli tom kutu nasuprotnu stranicu u omjeru preostalih stranica. Za naš trokut to znači da vrijedi  , odnosno
, odnosno  . Iz svega do sada možemo izračunati
. Iz svega do sada možemo izračunati  i
i  u ovisnosti o
u ovisnosti o  ,
,  i
i  .
.

Još moramo uzeti u obzir pretpostavku  da dobijemo
da dobijemo  ,
,  .
.
Budući da je  središte kružnice upisane trokutu
središte kružnice upisane trokutu  , pravac
, pravac 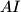 je simetrala kuta
je simetrala kuta 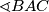 , što je unutarnji kut trokuta
, što je unutarnji kut trokuta  , ali i trokuta
, ali i trokuta 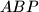 . Ponovno možemo iskoristiti trik s podjelom u omjeru stranica da dobijemo
. Ponovno možemo iskoristiti trik s podjelom u omjeru stranica da dobijemo  Budući da vrijedi
Budući da vrijedi  , slijedi da je
, slijedi da je  .
.
Za bod upišite odgovor na pitanje mora li središte trokutu upisane kružnice uvijek biti unutar trokuta (DA ili NE).
\textbf{Središte kružnice upisane trokutu}
Za sljedeću karakterističnu točku trebat će nam simetrala kuta, pa istaknimo ponovno jednu bitnu činjenicu.
\textbf{Propozicija}\\
Točka leži na simetrali kuta ako i samo ako je jednako udaljena od njegovih krakova.
Primijetite da ponovno možemo zaključivati u oba smjera.
\textbf{Definicija}\\
Središte kružnice upisane trokutu $ABC$ sjecište je simetrala kuteva trokuta $ABC$.
\begin{center}
\includegraphics[scale=0.5]{upisana.png}
\end{center}
Ovaj puta naša karakteristična točka mora biti unutar trokuta neovisno o tome kakav trokut promatramo. Također, ponovno pronalazimo tetivne četverokute: polumjer i tangenta u točki iz koje promatramo polumjer moraju biti okomiti pa ponovno imamo puno pravih kuteva.
Uočimo i da imamo neke jednakosti duljina. Označimo redom s $D$, $E$, $F$ točke u kojima upisana kružnica dira stranice $\overline{AB}$, $\overline{BC}$ i $\overline{CA}$. Tada po poučku KSK možemo zaključiti da su čak tri para trokuta sukladni: $ADI\cong AFI$, $BDI\cong BEI$ i $CFI\cong CEI$, odakle zaključujemo i da vrijedi $|AD|=|AF|$, $|BD|=|BE|$ i $|CF|=|CE|$.
Središte upisane kružnice najčešće označavamo slovom $I$, a dokaz da se simetrale svih triju stranica trokuta sijeku u jednoj točki možete vidjeti \href{https://artofproblemsolving.com/wiki/index.php/Incenter}{ovdje}.
\textbf{Primjer}\\
Neka je $ABC$ trokut za koji vrijedi $|AB|+|BC|=2|AC|$. Neka je $P$ sjecište simetrale kuta $\sphericalangle ABC$ sa stranicom $\overline{AC}$, a $I$ središte trokutu $ABC$ upisane kružnice.\\
Odredite omjer $|IP| : |BP|$.
\textit{Rješenje:}\\
Označimo $|AP|=x$ i $CP=y$, te označimo standardno stranice $|BC|=a$, $|CA|=b$ i $|AB|=c$. Uvjet zadatka sada možemo zapisati kao $a+c=2b$, a znamo i da vrijedi $x+y=b$.
\begin{center}
\includegraphics[scale=0.5]{upisana_pr.png}
\end{center}
Prisjetimo se, simetrala unutarnjeg kuta trokuta dijeli tom kutu nasuprotnu stranicu u omjeru preostalih stranica. Za naš trokut to znači da vrijedi $x:y = c:a$, odnosno $x=y\frac{c}{a}$. Iz svega do sada možemo izračunati $x$ i $y$ u ovisnosti o $a$, $b$ i $c$.
$$b=x+y \implies b=y\frac{c}{a} + y \implies y\left( \frac{c+a}{a} \right) = b \implies y=\frac{ab}{a+c} \implies x=\frac{bc}{a+c}$$
Još moramo uzeti u obzir pretpostavku $a+c=2b$ da dobijemo $x=\frac c2$, $y=\frac a2$.
Budući da je $I$ središte kružnice upisane trokutu $ABC$, pravac $AI$ je simetrala kuta $\sphericalangle BAC$, što je unutarnji kut trokuta $ABC$, ali i trokuta $ABP$. Ponovno možemo iskoristiti trik s podjelom u omjeru stranica da dobijemo $$|PI|:|IB| = x:c = \frac{c}{2} : c = 1:2.$$
Budući da vrijedi $|BP|=|PI|+|IB|$, slijedi da je $|IP| : |BP| = 1:3$.
Za bod upišite odgovor na pitanje mora li središte trokutu upisane kružnice uvijek biti unutar trokuta (DA ili NE).
 sjecište je simetrala kuteva trokuta
sjecište je simetrala kuteva trokuta  .
. 
 ,
,  ,
,  točke u kojima upisana kružnica dira stranice
točke u kojima upisana kružnica dira stranice  ,
,  i
i  . Tada po poučku KSK možemo zaključiti da su čak tri para trokuta sukladni:
. Tada po poučku KSK možemo zaključiti da su čak tri para trokuta sukladni:  ,
,  i
i  , odakle zaključujemo i da vrijedi
, odakle zaključujemo i da vrijedi  ,
,  i
i  .
. , a dokaz da se simetrale svih triju stranica trokuta sijeku u jednoj točki možete vidjeti ovdje.
, a dokaz da se simetrale svih triju stranica trokuta sijeku u jednoj točki možete vidjeti ovdje. trokut za koji vrijedi
trokut za koji vrijedi  . Neka je
. Neka je  sjecište simetrale kuta
sjecište simetrale kuta  sa stranicom
sa stranicom  , a
, a  središte trokutu
središte trokutu  upisane kružnice.
upisane kružnice. .
. i
i  , te označimo standardno stranice
, te označimo standardno stranice 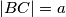 ,
, 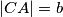 i
i 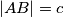 . Uvjet zadatka sada možemo zapisati kao
. Uvjet zadatka sada možemo zapisati kao  , a znamo i da vrijedi
, a znamo i da vrijedi  .
. 
 , odnosno
, odnosno  . Iz svega do sada možemo izračunati
. Iz svega do sada možemo izračunati  i
i  u ovisnosti o
u ovisnosti o  ,
,  i
i  .
.
 da dobijemo
da dobijemo  ,
,  .
. središte kružnice upisane trokutu
središte kružnice upisane trokutu  , pravac
, pravac 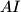 je simetrala kuta
je simetrala kuta 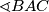 , što je unutarnji kut trokuta
, što je unutarnji kut trokuta  , ali i trokuta
, ali i trokuta 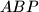 . Ponovno možemo iskoristiti trik s podjelom u omjeru stranica da dobijemo
. Ponovno možemo iskoristiti trik s podjelom u omjeru stranica da dobijemo  Budući da vrijedi
Budući da vrijedi  , slijedi da je
, slijedi da je  .
.