Težište
Kako bismo definirali težište, trebaju nam težišnice.
Definicija
Težišnica trokuta je dužina koja spaja vrh trokuta s polovištem nasuprotne stranice.
Naravno, svaki trokut ima tri težišnice.
Definicija
Težište trokuta  sjecište je težišnica trokuta
sjecište je težišnica trokuta  .
.
Težište najčešće označavamo slovom  , a dokaz da se simetrale svih triju stranica trokuta sijeku u jednoj točki možete vidjeti ovdje.
, a dokaz da se simetrale svih triju stranica trokuta sijeku u jednoj točki možete vidjeti ovdje.
Jako bitna činjenica vezana uz težište trokuta (koju ćemo puno i koristiti) je sljedeća:
Propozicija
Udaljenost težišta od pojedinog vrha trokuta jednaka je 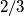 duljine odgovarajuće težišnice.
duljine odgovarajuće težišnice.
Drugim riječima, težište dijeli svaku težišnicu u omjeru 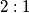 gledajući od vrha prema polovištu.
gledajući od vrha prema polovištu.
Primjer
Na slici su prikazane tri sukladne male kružnice koje se međusobno dodiruju i koje iznutra dodiruju veliku kružnicu sa središtem  . Izračunajte polumjer velike kružnice ako je polumjer male kružnice jednak
. Izračunajte polumjer velike kružnice ako je polumjer male kružnice jednak  cm.
cm.
Rješenje:
Primijetimo da središta manjih kružnica tvore jednakostraničan trokut i to takav da je  baš težište tog trokuta. Duljina dužine koja spaja
baš težište tog trokuta. Duljina dužine koja spaja  s nekim vrhom tog trokuta jednaka je
s nekim vrhom tog trokuta jednaka je  duljine težišnice tog jednakokračnog trokuta, a budući da je trokut jednakostraničan, njegove težišnice i visine iste su duljine.
duljine težišnice tog jednakokračnog trokuta, a budući da je trokut jednakostraničan, njegove težišnice i visine iste su duljine.
Male sukladne kružnice se međusobno dodiruju pa je duljina stranice jednakostraničnog trokuta jednaka duljini dva polumjera malih kružnica, odnosno  cm. Duljina visine jednakostraničnog trokuta jednaka je
cm. Duljina visine jednakostraničnog trokuta jednaka je 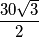 cm
cm 
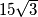 cm, pa zaključujemo da duljina dužine koja spaja
cm, pa zaključujemo da duljina dužine koja spaja  i središte male kružnice (odnosno težište i vrh jednakostraničnog trokuta) mora biti jednaka
i središte male kružnice (odnosno težište i vrh jednakostraničnog trokuta) mora biti jednaka 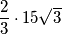 cm
cm 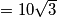 cm.
cm.
Polumjer velike kružnice sada možemo dobiti kao zbroj udaljenosti težišta  od središta male kružnice i polumjera male kružnice. Dakle, traženi polumjer velike kružnice jednak je
od središta male kružnice i polumjera male kružnice. Dakle, traženi polumjer velike kružnice jednak je 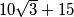 cm.
cm.
Ideja težišta zapravo nam dolazi iz fizike. Težište nekog tijela možemo zamisliti kao točku u kojoj je koncentrirana sva masa tog tijela. Zamislite da imate jako tanki metalni trokut, kako biste pronašli jednu točku u kojoj možete poduprijeti taj trokut kako bi stajao u ravnoteži? Ta točka je upravo težište trokuta!
Za bod upišite kako se zove dužina koja spaja polovišta dviju stranica trokuta (sve malim slovima).
\textbf{Težište}
Kako bismo definirali težište, trebaju nam težišnice.
\textbf{Definicija}\\
Težišnica trokuta je dužina koja spaja vrh trokuta s polovištem nasuprotne stranice.
Naravno, svaki trokut ima tri težišnice.
\textbf{Definicija}\\
Težište trokuta $ABC$ sjecište je težišnica trokuta $ABC$.
Težište najčešće označavamo slovom $T$, a dokaz da se simetrale svih triju stranica trokuta sijeku u jednoj točki možete vidjeti \href{https://artofproblemsolving.com/wiki/index.php/Centroid}{ovdje}.
Jako bitna činjenica vezana uz težište trokuta (koju ćemo puno i koristiti) je sljedeća:
\textbf{Propozicija}\\
Udaljenost težišta od pojedinog vrha trokuta jednaka je $2/3$ duljine odgovarajuće težišnice.
Drugim riječima, težište dijeli svaku težišnicu u omjeru $2:1$ gledajući od vrha prema polovištu.
\textbf{Primjer}\\
Na slici su prikazane tri sukladne male kružnice koje se međusobno dodiruju i koje iznutra dodiruju veliku kružnicu sa središtem $S$.
Izračunajte polumjer velike kružnice ako je polumjer male kružnice jednak $15$ cm.
\begin{center}
\includegraphics[scale=0.5]{imageG29.png}
\end{center}
\textit{Rješenje:}\\
Primijetimo da središta manjih kružnica tvore jednakostraničan trokut i to takav da je $S$ baš težište tog trokuta.
Duljina dužine koja spaja $S$ s nekim vrhom tog trokuta jednaka je $\dfrac{2}{3}$ duljine težišnice tog jednakokračnog trokuta, a budući da je trokut jednakostraničan, njegove težišnice i visine iste su duljine.
Male sukladne kružnice se međusobno dodiruju pa je duljina stranice jednakostraničnog trokuta jednaka duljini dva polumjera malih kružnica, odnosno $30$cm. Duljina visine jednakostraničnog trokuta jednaka je $\dfrac{30 \sqrt{3}}{2}$ cm $=$ $15 \sqrt{3}$cm, pa zaključujemo da duljina dužine koja spaja $S$ i središte male kružnice (odnosno težište i vrh jednakostraničnog trokuta) mora biti jednaka $\dfrac{2}{3} \cdot 15\sqrt{3}$ cm $ = 10 \sqrt{3} $ cm.
Polumjer velike kružnice sada možemo dobiti kao zbroj udaljenosti težišta $S$ od središta male kružnice i polumjera male kružnice. Dakle, traženi polumjer velike kružnice jednak je $10 \sqrt{3} + 15$~cm.
Ideja težišta zapravo nam dolazi iz fizike. Težište nekog tijela možemo zamisliti kao točku u kojoj je koncentrirana sva masa tog tijela. Zamislite da imate jako tanki metalni trokut, kako biste pronašli jednu točku u kojoj možete poduprijeti taj trokut kako bi stajao u ravnoteži? Ta točka je upravo težište trokuta!
Za bod upišite kako se zove dužina koja spaja polovišta dviju stranica trokuta (sve malim slovima).
 sjecište je težišnica trokuta
sjecište je težišnica trokuta  .
. , a dokaz da se simetrale svih triju stranica trokuta sijeku u jednoj točki možete vidjeti ovdje.
, a dokaz da se simetrale svih triju stranica trokuta sijeku u jednoj točki možete vidjeti ovdje.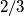 duljine odgovarajuće težišnice.
duljine odgovarajuće težišnice.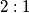 gledajući od vrha prema polovištu.
gledajući od vrha prema polovištu. . Izračunajte polumjer velike kružnice ako je polumjer male kružnice jednak
. Izračunajte polumjer velike kružnice ako je polumjer male kružnice jednak  cm.
cm. 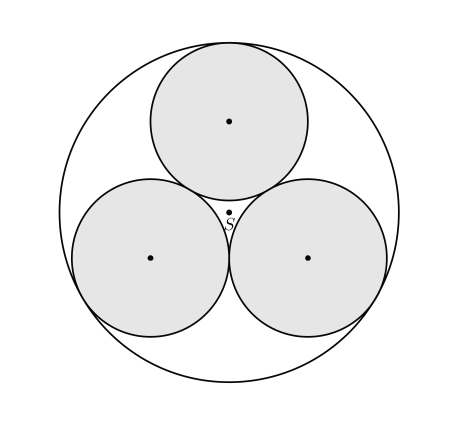
 baš težište tog trokuta. Duljina dužine koja spaja
baš težište tog trokuta. Duljina dužine koja spaja  s nekim vrhom tog trokuta jednaka je
s nekim vrhom tog trokuta jednaka je  duljine težišnice tog jednakokračnog trokuta, a budući da je trokut jednakostraničan, njegove težišnice i visine iste su duljine.
duljine težišnice tog jednakokračnog trokuta, a budući da je trokut jednakostraničan, njegove težišnice i visine iste su duljine. cm. Duljina visine jednakostraničnog trokuta jednaka je
cm. Duljina visine jednakostraničnog trokuta jednaka je 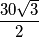 cm
cm 
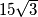 cm, pa zaključujemo da duljina dužine koja spaja
cm, pa zaključujemo da duljina dužine koja spaja  i središte male kružnice (odnosno težište i vrh jednakostraničnog trokuta) mora biti jednaka
i središte male kružnice (odnosno težište i vrh jednakostraničnog trokuta) mora biti jednaka 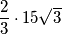 cm
cm 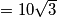 cm.
cm. od središta male kružnice i polumjera male kružnice. Dakle, traženi polumjer velike kružnice jednak je
od središta male kružnice i polumjera male kružnice. Dakle, traženi polumjer velike kružnice jednak je 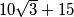 cm.
cm.