MetaMath '24

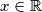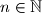\textbf{Zadatak:} Za $x\in \mathbb{R}$ i $n\in \mathbb{N}$, postoji racionalan broj $\frac{p}{q}$ i $1 \leq q \leq n$ takav da $$ \bigg|x-\frac{p}{q}\bigg|< \frac{1}{nq}.$$ \textbf{Rješenje:}\\ Množenjem s $q$ dobivamo $|xq-p| < \frac{1}{n}$, sada vidimo da tražimo $q$ tako da je $xq$ "jako blizu" cijelog broja. Zato promatramo $\{xq\}$ decimalni dio broja $xq$ i intervale $[0, \frac{1}{n}), [\frac{1}{n}, \frac{2}{n}), \dots, [\frac{n-1}{n}, 1)$. \\\\ Pomoću Dirichletovog principa ćemo pokazati da postoji $q$ takav da je $\{xq\} < \frac{1}{n}$. Promatramo $\{xa\}$ za $0 \leq a \leq n$, po Dirichletovom principu postoje $a < a'$ koji se nalaze u istom intervalu pa za $q = a'-a$ vrijedi $\{xq\} < \frac{1}{n}$. Za $p = xq-\{xq\}$ se postiže tvrdnja.\\\\ Koristili smo kombinatorni pristup kako bi pokazali da traženi brojevi postoje bez da ih eksplicitno odredimo. Za nastavak: u 6 tjedana je točno 10! sekundi (upišite 1 za točno ili 0 za netočno).