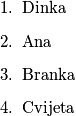Logičko-kombinatorni zadatci čine jedno veliko područje natjecateljske matematike. Zato ćemo u sljedećih par zadataka i njihovih rješenja pokazati nekoliko metoda kako pristupati zadatcima logičkog tipa.
Zadatak. Četiri prijateljice, Ana, Branka, Cvijeta i Dinka, odigrale su turnir u stolnom tenisu. Na kraju je stigla Erika i zanimala se za konačni poredak. U nadvikivanju prijateljica uspjela je čuti ova tri odgovora: 
Naknadno, kad je napokon saznala ispravan poredak, Erika je primijetila da je u svakoj izjavi jedan dio istinit, a drugi neistinit.
Koji je ispravan poredak igračica?
Rješenje. Ideja je tretirati jednu po jednu pretpostavku kao istinitu, a zatim utvrditi udovoljava li ta pretpostavka sve uvjete zadatka, tj. slaže li se s ostalim izjavama. Ako da, tada je istinita, a ako ne, tada nije istinita.
Pretpostavimo recimo da je prvi dio prve izjave ,,Dinka je bila druga, a Branka treća'' istinit, dakle gledajmo što vrijedi ako je Dinka druga. Onda je jasno da Ana nije druga. Gledajmo sada drugu izjavu ,,Branka je bila četvrta, a Ana druga". Znamo da drugi dio nije istinit u ovom slučaju. Stoga prvi dio izjave mora biti istinit, tj. vrijedi da je Branka četvrta.
Slično, u trećoj izjavi ,,Cvijeta je bila druga, a Dinka je pobijedila'' znamo da prvi dio nije istinit, pa drugi dio mora biti istinit, tj. Dinka je prva. Hmm ček ček, što!? Zar nije Dinka druga? I prva i druga istovremeno?! Neće ići! Došli smo do nečeg što u matematici zovemo kontradikcija, tj. proturječje.
Krenuli smo od pretpostavke da je Dinka bila druga i došli do kontradikcije. Jako je važno da je svaki zaključak iz početne pretpostavke bio logički ispravan, dakle nismo došli do kontradikcije zato što smo napravili neku logičku grešku u zaključivanju. Ne, sve je bilo ispravno, ali stvari se ipak ne poklapaju na kraju. Zato možemo zaključiti da početna pretpostavka, za koju jedino nismo sigurni da je ispravna, ustvari nije bila istinita!
Sada možemo napraviti neke zaključke. Kako je prvi dio prve izjave neistinit, drugi dio te izjave mora biti istinit, tj. Branka je bila treća. Tada je prvi dio treće izjave netočan, pa drugi dio iste izjave mora biti ispravan, dakle Ana je druga. Sada možemo zaključiti da prvi dio treće izjave ne može biti istinit, pa drugi dio te izjave mora biti istinit, dakle Dinka je doista pobijedila.
Sada znamo kako izglelda konačni poredak: 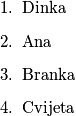
Kao rješenje upišite ime pobjednice.
\textbf{Logičko-kombinatorni zadatci} čine jedno veliko područje natjecateljske matematike. Zato ćemo u sljedećih par zadataka i njihovih rješenja pokazati nekoliko metoda kako pristupati zadatcima logičkog tipa.
\textbf{Zadatak.} Četiri prijateljice, Ana, Branka, Cvijeta i Dinka, odigrale su turnir u stolnom tenisu. Na kraju je stigla Erika i zanimala se za konačni poredak. U nadvikivanju prijateljica uspjela je čuti ova tri odgovora:
\begin{enumerate}
\item ,,Dinka je bila druga, a Branka treća!''
\item ,,Branka je bila četvrta, a Ana druga!''
\item ,,Cvijeta je bila druga, a Dinka je pobijedila!''
\end{enumerate}
Naknadno, kad je napokon saznala ispravan poredak, Erika je primijetila da je u svakoj izjavi jedan dio istinit, a drugi neistinit.
Koji je ispravan poredak igračica?
\textbf{Rješenje.} Ideja je tretirati jednu po jednu pretpostavku kao istinitu, a zatim utvrditi udovoljava li ta pretpostavka sve uvjete zadatka, tj. slaže li se s ostalim izjavama. Ako da, tada je istinita, a ako ne, tada nije istinita.
Pretpostavimo recimo da je prvi dio prve izjave ,,\textit{Dinka je bila druga, a Branka treća}'' istinit, dakle gledajmo što vrijedi ako je \textbf{Dinka druga}. Onda je jasno da Ana nije druga. Gledajmo sada drugu izjavu ,,\textit{Branka je bila četvrta, a Ana druga}". Znamo da drugi dio nije istinit u ovom slučaju. Stoga prvi dio izjave mora biti istinit, tj. vrijedi da je \textbf{Branka četvrta}.
Slično, u trećoj izjavi ,,\textit{Cvijeta je bila druga, a Dinka je pobijedila}'' znamo da prvi dio nije istinit, pa drugi dio mora biti istinit, tj. \textbf{Dinka je prva}. Hmm ček ček, što!? Zar nije Dinka druga? I prva i druga istovremeno?! Neće ići! Došli smo do nečeg što u matematici zovemo \textit{kontradikcija}, tj. proturječje.
Krenuli smo od pretpostavke da je Dinka bila druga i došli do kontradikcije. Jako je važno da je svaki zaključak iz početne pretpostavke bio logički ispravan, dakle nismo došli do kontradikcije zato što smo napravili neku logičku grešku u zaključivanju. Ne, sve je bilo ispravno, ali stvari se ipak ne poklapaju na kraju. Zato možemo zaključiti da početna pretpostavka, za koju jedino nismo sigurni da je ispravna, ustvari nije bila istinita!
Sada možemo napraviti neke zaključke. Kako je prvi dio prve izjave neistinit, drugi dio te izjave mora biti istinit, tj. Branka je bila treća. Tada je prvi dio treće izjave netočan, pa drugi dio iste izjave mora biti ispravan, dakle Ana je druga. Sada možemo zaključiti da prvi dio treće izjave ne može biti istinit, pa drugi dio te izjave mora biti istinit, dakle Dinka je doista pobijedila.
Sada znamo kako izglelda konačni poredak:
\begin{enumerate}
\item Dinka
\item Ana
\item Branka
\item Cvijeta
\end{enumerate}
Kao rješenje upišite ime pobjednice.