Ivan i Mario igraju igru. Prvo Ivan kaže jedan prirodni broj do  , a zatim Mario tom broju doda broj koji nije veći od 10 i izgovara taj zbroj, zatim to isto napravi Ivan i tako naizmjence. Pobjednik je onaj igrač koji prvi izgovori broj
, a zatim Mario tom broju doda broj koji nije veći od 10 i izgovara taj zbroj, zatim to isto napravi Ivan i tako naizmjence. Pobjednik je onaj igrač koji prvi izgovori broj  . Može li Ivan odabrati brojeve tako da osigura pobjedu?
. Može li Ivan odabrati brojeve tako da osigura pobjedu?
Rješenje. Zadatak rješavamo unazad. Pitajmo se u kojem trenutku možemo reći broj  . Kada bi igrač prije nas rekao bilo koji broj od
. Kada bi igrač prije nas rekao bilo koji broj od 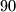 do
do 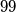 , tada bismo mogli tom broju dodati broj od
, tada bismo mogli tom broju dodati broj od  do
do  , zbrojiti i reći
, zbrojiti i reći  te tako pobijediti. Stoga razmislimo, u potezu prije toga, možemo li "natjerati" suparnika da kaže broj od
te tako pobijediti. Stoga razmislimo, u potezu prije toga, možemo li "natjerati" suparnika da kaže broj od 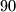 do
do 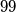 ?
?
Odgovor je da. Naime, ako bismo mi izrekli broj 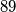 , tada suparnik najmanje može dodati
, tada suparnik najmanje može dodati  i reći
i reći 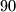 , a najviše dodati
, a najviše dodati  i reći
i reći 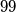 i tada pobjeđujemo.
i tada pobjeđujemo.
Sada cilj igrača više nije izreći  , nego izreći broj
, nego izreći broj 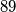 koji je pobjednički. To je moguće kada u našem prošlom potezu izrečemo
koji je pobjednički. To je moguće kada u našem prošlom potezu izrečemo 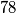 jer tada suparnik mora reći broj od
jer tada suparnik mora reći broj od 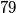 do
do 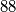 .
.
Dakle, 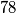 je pobjednički broj. Istim principom zaključujemo da su pobjednički brojevi i
je pobjednički broj. Istim principom zaključujemo da su pobjednički brojevi i 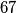 ,
, 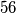 ,
, 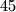 ,
, 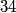 ,
, 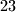 ,
,  i
i  . Kada god može igrač izreći pobjednički broj, on ima pobjedničku strategiju.
. Kada god može igrač izreći pobjednički broj, on ima pobjedničku strategiju.
Budući da je  pobjednički broj, to je broj koji može izreći prvi igrač u prvom potezu, stoga Ivan ima pobjedničku strategiju.
pobjednički broj, to je broj koji može izreći prvi igrač u prvom potezu, stoga Ivan ima pobjedničku strategiju.
Kao rješenje upišite ukupan broj poteza koji će se odigrati tijekom igre ako Ivan igra pobjednički.
Ivan i Mario igraju igru. Prvo Ivan kaže jedan prirodni broj do $10$, a zatim Mario tom broju doda broj koji nije veći od 10 i izgovara taj zbroj, zatim to isto napravi Ivan i tako naizmjence. Pobjednik je onaj igrač koji prvi izgovori broj $100$. Može li Ivan odabrati brojeve tako da osigura pobjedu? \\\\
\textit{Rješenje.} Zadatak rješavamo unazad. Pitajmo se u kojem trenutku možemo reći broj $100$. Kada bi igrač prije nas rekao bilo koji broj od $90$ do $99$, tada bismo mogli tom broju dodati broj od $1$ do $10$, zbrojiti i reći $100$ te tako pobijediti. Stoga razmislimo, u potezu prije toga, možemo li "natjerati" suparnika da kaže broj od $90$ do $99$? \\\\
Odgovor je da. Naime, ako bismo mi izrekli broj $89$, tada suparnik najmanje može dodati $1$ i reći $90$, a najviše dodati $10$ i reći $99$ i tada pobjeđujemo.
\\\\
Sada cilj igrača više nije izreći $100$, nego izreći broj $89$ koji je \textit{pobjednički}. To je moguće kada u našem prošlom potezu izrečemo $78$ jer tada suparnik mora reći broj od $79$ do $88$.
\\\\
Dakle, $78$ je \textit{pobjednički} broj. Istim principom zaključujemo da su \textit{pobjednički} brojevi i $67$, $56$, $45$, $34$, $23$, $12$ i $1$. Kada god može igrač izreći \textit{pobjednički} broj, on ima \textbf{pobjedničku strategiju}.
\\\\
Budući da je $1$ \textit{pobjednički} broj, to je broj koji može izreći prvi igrač u prvom potezu, stoga Ivan ima \textbf{pobjedničku strategiju}. \\\\
Kao rješenje upišite ukupan broj poteza koji će se odigrati tijekom igre ako Ivan igra \textit{pobjednički}.
 , a zatim Mario tom broju doda broj koji nije veći od 10 i izgovara taj zbroj, zatim to isto napravi Ivan i tako naizmjence. Pobjednik je onaj igrač koji prvi izgovori broj
, a zatim Mario tom broju doda broj koji nije veći od 10 i izgovara taj zbroj, zatim to isto napravi Ivan i tako naizmjence. Pobjednik je onaj igrač koji prvi izgovori broj  . Može li Ivan odabrati brojeve tako da osigura pobjedu?
. Može li Ivan odabrati brojeve tako da osigura pobjedu?  . Kada bi igrač prije nas rekao bilo koji broj od
. Kada bi igrač prije nas rekao bilo koji broj od 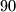 do
do 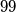 , tada bismo mogli tom broju dodati broj od
, tada bismo mogli tom broju dodati broj od  do
do  , zbrojiti i reći
, zbrojiti i reći  te tako pobijediti. Stoga razmislimo, u potezu prije toga, možemo li "natjerati" suparnika da kaže broj od
te tako pobijediti. Stoga razmislimo, u potezu prije toga, možemo li "natjerati" suparnika da kaže broj od 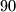 do
do 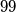 ?
? 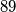 , tada suparnik najmanje može dodati
, tada suparnik najmanje može dodati  i reći
i reći 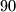 , a najviše dodati
, a najviše dodati  i reći
i reći 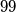 i tada pobjeđujemo.
i tada pobjeđujemo.  , nego izreći broj
, nego izreći broj 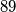 koji je pobjednički. To je moguće kada u našem prošlom potezu izrečemo
koji je pobjednički. To je moguće kada u našem prošlom potezu izrečemo 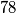 jer tada suparnik mora reći broj od
jer tada suparnik mora reći broj od 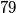 do
do 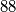 .
. 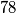 je pobjednički broj. Istim principom zaključujemo da su pobjednički brojevi i
je pobjednički broj. Istim principom zaključujemo da su pobjednički brojevi i 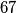 ,
, 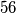 ,
, 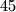 ,
, 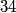 ,
, 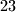 ,
,  i
i  . Kada god može igrač izreći pobjednički broj, on ima pobjedničku strategiju.
. Kada god može igrač izreći pobjednički broj, on ima pobjedničku strategiju.  pobjednički broj, to je broj koji može izreći prvi igrač u prvom potezu, stoga Ivan ima pobjedničku strategiju.
pobjednički broj, to je broj koji može izreći prvi igrač u prvom potezu, stoga Ivan ima pobjedničku strategiju. 