Razred se sastoji od  učenika. Dokaži da u tom razredu sigurno postoje barem dva učenika koji su rođeni u istom mjesecu.
učenika. Dokaži da u tom razredu sigurno postoje barem dva učenika koji su rođeni u istom mjesecu.
Rješenje. Zadatci u kojima se traži da se dokaže neka tvrdnja mogu djelovati neobično. Što se misli pod dokaži? Je li ovo uopće matematika, ili je neka filozofija/logika? Gdje je tu računanje, rješavanje jednadžbi?
Matematika je (srećom) puno više od računanja i rješavanja jednadžbi, općenito puno više od ,,igranja s brojevima''. Kao prvo, igramo se mi i s točkama i svakakvim linijama! Kao drugo, u matematici se općenito bavimo raznim izjavama i zaključcima, koji se istini za volju uglavnom odnose na matematičke objekte, kao što su (naravno) brojevi, skupovi i svakakvi geometrijski objekti. Evo i nekih primjera: 
Dokazati neku izjavu znači koristiti ispravno logičko zaključivanje kako bismo iz nekih poznatih istinitih činjenica zaključili da je navedena izjava također istinita.
Vratimo se sada našem zadatku. Kako bismo ga riješili, koristit ćemo jednu posebnu metodu dokazivanja, koja ,,kreće s kraja", a zove se metoda kontradikcije, ili po hrvatski proturječja. Najprije ćemo pretpostaviti da tvrdnja koju želimo dokazati nije ispravna. Zvuči čudno, ali zapravo to stalno radimo kada nešto želimo analizirati ili donijeti neku odluku. Trebam li učiti za ispit iz povijesti ili ću samo rješavati matematičke zadatke? Pa ako ne budem učio/la povijest, postoji velika vjerojatnost da u tom slučaju dobijem negativnu ocjenu. Onda ću ionako morati učiti za ispraviti tu ocjenu, pa si nisam baš olakšao/la život. A i neugodno je dobiti negativno. Dakle, ne sviđa mi se što se dogodi ako ne učim povijest - moram dakle zaključiti da je ipak bolje da malo prelistam udžbenik iz povijesti.
U našem zadatku, pretpostavimo da je svaki učenik rođen u različitom mjesecu.
Budući da ima  različitih učenika, a svi su rođeni u različitom mjesecu, znači da bi u kalendaru trebalo biti barem
različitih učenika, a svi su rođeni u različitom mjesecu, znači da bi u kalendaru trebalo biti barem  različitih mjeseci. Ali ovo je naravno besmislica! (Barem s trenutnim kalendarom. Možda ne bi bilo ni loše da imamo 13 mjeseci. Tada bi svaki mjesec mogao trajati
različitih mjeseci. Ali ovo je naravno besmislica! (Barem s trenutnim kalendarom. Možda ne bi bilo ni loše da imamo 13 mjeseci. Tada bi svaki mjesec mogao trajati 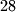 dana, koliko i otprilike treba Mjesecu da obiđe Zemlju i svaki mjesec bi imao točno
dana, koliko i otprilike treba Mjesecu da obiđe Zemlju i svaki mjesec bi imao točno  tjedna. Nedostajalo bi nam
tjedna. Nedostajalo bi nam 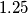 dana u godini, ali to je sitnica, ionako gubimo puno vremena na svakakve gluposti). Time smo došli do naše kontradikcije.
dana u godini, ali to je sitnica, ionako gubimo puno vremena na svakakve gluposti). Time smo došli do naše kontradikcije.
Sada se možemo vratiti na početak i reći da je početna pretpostavka da je svaki učenik rođen u različitom mjesecu netočna, jer nas je dovela do protuslovlja. Stoga postoje barem dva učenika rođena u istom mjesecu, a to je trebalo i dokazati. Primijeti da i dalje ne znamo koji je to mjesec, kao ni koliko točno, a naravno ne i koji učenici su rođeni u tom mjesecu - to bi već bilo previše. Znamo samo da takav mjesec i takvi učenici sigurno postoje, koji god on bili.
Kao rješenje upiši koliko najmanje učenika treba biti u razredu da možemo garantirati da postoje barem tri rođena u istom mjesecu.
Razred se sastoji od $13$ učenika. Dokaži da u tom razredu sigurno postoje barem dva učenika koji su rođeni u istom mjesecu.
\textbf{Rješenje.} Zadatci u kojima se traži da se \textit{dokaže} neka tvrdnja mogu djelovati neobično. Što se misli pod dokaži? Je li ovo uopće matematika, ili je neka filozofija/logika? Gdje je tu računanje, rješavanje jednadžbi?
Matematika je (srećom) puno više od računanja i rješavanja jednadžbi, općenito puno više od ,,igranja s brojevima''. Kao prvo, igramo se mi i s točkama i svakakvim linijama! Kao drugo, u matematici se općenito bavimo raznim izjavama i zaključcima, koji se istini za volju uglavnom odnose na matematičke objekte, kao što su (naravno) brojevi, skupovi i svakakvi geometrijski objekti. Evo i nekih primjera:
\begin{itemize}
\item $5$ je prirodan broj; $1$ je najmanji prirodan broj; $9999999999999$ je najveći prirodan broj (tko je rekao da matematičke izjave moraju biti točne ;)
\item $2 + 2 = 4$; $10 < 10^2$
\item ako je prirodan broj $n$ djeljiv sa $6$, tada je i broj $n + 24$ djeljiv sa $6$
\item svakom trokutu može se opisati točno jedna kružnica
\item itd. itd.
\end{itemize}
\textbf{Dokazati neku izjavu znači koristiti ispravno logičko zaključivanje kako bismo iz nekih poznatih istinitih činjenica zaključili da je navedena izjava također istinita.}
Vratimo se sada našem zadatku. Kako bismo ga riješili, koristit ćemo jednu posebnu metodu dokazivanja, koja ,,kreće s kraja", a zove se metoda \textbf{kontradikcije}, ili po hrvatski \textbf{proturječja}. Najprije ćemo \textit{pretpostaviti da tvrdnja koju želimo dokazati nije ispravna}. Zvuči čudno, ali zapravo to stalno radimo kada nešto želimo analizirati ili donijeti neku odluku. Trebam li učiti za ispit iz povijesti ili ću samo rješavati matematičke zadatke? Pa \textbf{ako ne budem učio/la povijest}, postoji velika vjerojatnost da u tom slučaju dobijem negativnu ocjenu. Onda ću ionako morati učiti za ispraviti tu ocjenu, pa si nisam baš olakšao/la život. A i neugodno je dobiti negativno. Dakle, ne sviđa mi se što se dogodi ako ne učim povijest - moram dakle zaključiti da je ipak bolje da malo prelistam udžbenik iz povijesti.
U našem zadatku, pretpostavimo da je svaki učenik rođen u različitom mjesecu.
Budući da ima $13$ različitih učenika, a svi su rođeni u različitom mjesecu, znači da bi u kalendaru trebalo biti barem $13$ različitih mjeseci. Ali ovo je naravno besmislica! (Barem s trenutnim kalendarom. Možda ne bi bilo ni loše da imamo 13 mjeseci. Tada bi svaki mjesec mogao trajati $28$ dana, koliko i otprilike treba Mjesecu da obiđe Zemlju i svaki mjesec bi imao točno $4$ tjedna. Nedostajalo bi nam $1.25$ dana u godini, ali to je sitnica, ionako gubimo puno vremena na svakakve gluposti). Time smo došli do naše kontradikcije.
Sada se možemo vratiti na početak i reći da je početna pretpostavka da je svaki učenik rođen u različitom mjesecu netočna, jer nas je dovela do protuslovlja. Stoga postoje barem dva učenika rođena u istom mjesecu, a to je trebalo i dokazati. Primijeti da i dalje ne znamo koji je to mjesec, kao ni koliko točno, a naravno ne i koji učenici su rođeni u tom mjesecu - to bi već bilo previše. Znamo samo da takav mjesec i takvi učenici sigurno postoje, koji god on bili.
Kao rješenje upiši koliko najmanje učenika treba biti u razredu da možemo garantirati da postoje barem tri rođena u istom mjesecu.
 učenika. Dokaži da u tom razredu sigurno postoje barem dva učenika koji su rođeni u istom mjesecu.
učenika. Dokaži da u tom razredu sigurno postoje barem dva učenika koji su rođeni u istom mjesecu.
 različitih učenika, a svi su rođeni u različitom mjesecu, znači da bi u kalendaru trebalo biti barem
različitih učenika, a svi su rođeni u različitom mjesecu, znači da bi u kalendaru trebalo biti barem  različitih mjeseci. Ali ovo je naravno besmislica! (Barem s trenutnim kalendarom. Možda ne bi bilo ni loše da imamo 13 mjeseci. Tada bi svaki mjesec mogao trajati
različitih mjeseci. Ali ovo je naravno besmislica! (Barem s trenutnim kalendarom. Možda ne bi bilo ni loše da imamo 13 mjeseci. Tada bi svaki mjesec mogao trajati 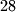 dana, koliko i otprilike treba Mjesecu da obiđe Zemlju i svaki mjesec bi imao točno
dana, koliko i otprilike treba Mjesecu da obiđe Zemlju i svaki mjesec bi imao točno  tjedna. Nedostajalo bi nam
tjedna. Nedostajalo bi nam 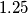 dana u godini, ali to je sitnica, ionako gubimo puno vremena na svakakve gluposti). Time smo došli do naše kontradikcije.
dana u godini, ali to je sitnica, ionako gubimo puno vremena na svakakve gluposti). Time smo došli do naše kontradikcije.