Dano je  prirodnih brojeva. Dokaži da se između njih mogu odabrati
prirodnih brojeva. Dokaži da se između njih mogu odabrati  broja čija je razlika djeljiva s
broja čija je razlika djeljiva s  .
.
Rješenje. Pri dijeljenju nekog prirodnog broja s  , moguće je dobiti
, moguće je dobiti  različitih ostataka:
različitih ostataka:  ,
,  ,
,  ,
,  ,...,
,...,  ,
, 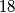 .
.
Slično kao i u jednom od prethodnih primjera, pretpostavimo suprotno, da svaki od  danih prirodnih brojeva daje različiti ostatak pri dijeljenju s
danih prirodnih brojeva daje različiti ostatak pri dijeljenju s  . To bi značilo da postoji
. To bi značilo da postoji  različitih ostataka pri dijeljenju s
različitih ostataka pri dijeljenju s  , no to je netočno (kontradikcija). Stoga barem dva broja daju isti ostatak pri dijeljenju s
, no to je netočno (kontradikcija). Stoga barem dva broja daju isti ostatak pri dijeljenju s  , a njihova razlika je tada djeljiva s
, a njihova razlika je tada djeljiva s  .
.
Slijedi i malo detaljniji raspis te činjenice. Znamo da se broj  djeljiv s
djeljiv s  može napisati u obliku
može napisati u obliku 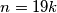 , gdje je
, gdje je  cijeli broj. Tada se neki drugi broj
cijeli broj. Tada se neki drugi broj  koji pri dijeljenju s
koji pri dijeljenju s  daje ostatak
daje ostatak  može napisati kao
može napisati kao 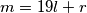 , gdje je
, gdje je  cijeli broj i
cijeli broj i 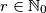 , manji od
, manji od  .
.
Označimo sa  i
i  ta dva broja. Budući da daju isti ostatak
ta dva broja. Budući da daju isti ostatak  pri dijeljenju s
pri dijeljenju s  , možemo pisati:
, možemo pisati: 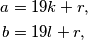 gdje su
gdje su  i
i  cijeli brojevi, a
cijeli brojevi, a 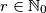 ,
, 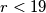 . Oduzimanjem ta dva broja dobivamo:
. Oduzimanjem ta dva broja dobivamo: 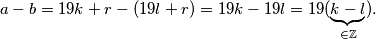 Stoga je ta razlika djeljiva s
Stoga je ta razlika djeljiva s  .
.
Kao rješenje upiši broj nenegativnih cijelih brojeva manjih od  .- to su ujedno i svi mogući ostatci pri dijeljenju s
.- to su ujedno i svi mogući ostatci pri dijeljenju s  .
.
Dano je $20$ prirodnih brojeva. Dokaži da se između njih mogu odabrati $2$ broja čija je razlika djeljiva s $19$. \\\\
\textbf{Rješenje.} Pri dijeljenju nekog prirodnog broja s $19$, moguće je dobiti $19$ različitih ostataka: $0$, $1$, $2$, $3$,..., $17$, $18$. \\\\
Slično kao i u jednom od prethodnih primjera, pretpostavimo suprotno, da svaki od $20$ danih prirodnih brojeva daje različiti ostatak pri dijeljenju s $19$. To bi značilo da postoji $20$ različitih ostataka pri dijeljenju s $19$, no to je netočno (\textbf{kontradikcija}). Stoga barem dva broja daju isti ostatak pri dijeljenju s $19$, a njihova razlika je tada djeljiva s $19$.
\\\\
Slijedi i malo detaljniji raspis te činjenice. Znamo da se broj $n$ djeljiv s $19$ može napisati u obliku $n=19k$, gdje je $k$ cijeli broj. Tada se neki drugi broj $m$ koji pri dijeljenju s $19$ daje ostatak $r$ može napisati kao $m=19l+r$, gdje je $l$ cijeli broj i $r\in \mathbb{N}_0$, manji od $19$. \\\\
Označimo sa $a$ i $b$ ta dva broja. Budući da daju isti ostatak $r$ pri dijeljenju s $19$, možemo pisati:
\begin{align*}
a&=19k+r, \\
b&=19l+r,
\end{align*}
gdje su $k$ i $l$ cijeli brojevi, a $r\in \mathbb{N}_0$, $r<19$. Oduzimanjem ta dva broja dobivamo:
$$
a-b=19k+r-(19l+r)=19k-19l=19(\underbrace{k-l}_{\in \mathbb{Z}}).
$$
Stoga je ta razlika djeljiva s $19$.
\\\\
Kao rješenje upiši broj nenegativnih cijelih brojeva manjih od $19$ .- to su ujedno i svi mogući ostatci pri dijeljenju s $19$.
 prirodnih brojeva. Dokaži da se između njih mogu odabrati
prirodnih brojeva. Dokaži da se između njih mogu odabrati  broja čija je razlika djeljiva s
broja čija je razlika djeljiva s  .
.  , moguće je dobiti
, moguće je dobiti  različitih ostataka:
različitih ostataka:  ,
,  ,
,  ,
,  ,...,
,...,  ,
, 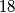 .
.  danih prirodnih brojeva daje različiti ostatak pri dijeljenju s
danih prirodnih brojeva daje različiti ostatak pri dijeljenju s  . To bi značilo da postoji
. To bi značilo da postoji  različitih ostataka pri dijeljenju s
različitih ostataka pri dijeljenju s  , no to je netočno (kontradikcija). Stoga barem dva broja daju isti ostatak pri dijeljenju s
, no to je netočno (kontradikcija). Stoga barem dva broja daju isti ostatak pri dijeljenju s  , a njihova razlika je tada djeljiva s
, a njihova razlika je tada djeljiva s  .
.  djeljiv s
djeljiv s  može napisati u obliku
može napisati u obliku 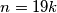 , gdje je
, gdje je  cijeli broj. Tada se neki drugi broj
cijeli broj. Tada se neki drugi broj  koji pri dijeljenju s
koji pri dijeljenju s  daje ostatak
daje ostatak  može napisati kao
može napisati kao 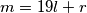 , gdje je
, gdje je  cijeli broj i
cijeli broj i 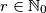 , manji od
, manji od  .
.  i
i  ta dva broja. Budući da daju isti ostatak
ta dva broja. Budući da daju isti ostatak  pri dijeljenju s
pri dijeljenju s  , možemo pisati:
, možemo pisati: 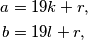 gdje su
gdje su  i
i  cijeli brojevi, a
cijeli brojevi, a 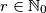 ,
, 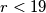 . Oduzimanjem ta dva broja dobivamo:
. Oduzimanjem ta dva broja dobivamo: 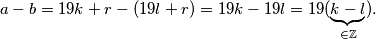 Stoga je ta razlika djeljiva s
Stoga je ta razlika djeljiva s  .
.  .- to su ujedno i svi mogući ostatci pri dijeljenju s
.- to su ujedno i svi mogući ostatci pri dijeljenju s  .
. 