Izračunaj: 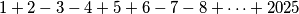 Rješenje. Uočimo pravilnost u ponavljanju pozitivnih i negativnih cijelih brojeva
Rješenje. Uočimo pravilnost u ponavljanju pozitivnih i negativnih cijelih brojeva 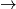 dva pozitivna, dva negativna, dva pozitivna, dva negativna, itd.
dva pozitivna, dva negativna, dva pozitivna, dva negativna, itd.
Također, vrijedi da je 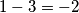 ,
, 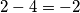 ,
, 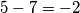 ,
, 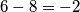 . Dakle, u toj jednoj grupi od 4 broja, prvi pozitivni i prvi negativni zbrojeni daju
. Dakle, u toj jednoj grupi od 4 broja, prvi pozitivni i prvi negativni zbrojeni daju  , isto kao i drugi pozitivni i drugi negativni. To znači da ta cijela grupa od
, isto kao i drugi pozitivni i drugi negativni. To znači da ta cijela grupa od  broja daje sumu
broja daje sumu 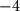 . Prikažimo zornije te grupe:
. Prikažimo zornije te grupe: 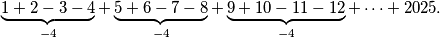 Moramo još dokučiti koliko takvih grupa ima. Uočimo da je posljednji broj svake grupe djeljiv s
Moramo još dokučiti koliko takvih grupa ima. Uočimo da je posljednji broj svake grupe djeljiv s  , a budući da je
, a budući da je 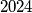 djeljiv s
djeljiv s  , posljednja grupa izgleda ovako:
, posljednja grupa izgleda ovako: 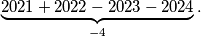 Dakle, grupiramo prvih
Dakle, grupiramo prvih 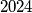 brojeva u grupe po
brojeva u grupe po  . Takvih grupa ima
. Takvih grupa ima 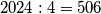 .
.
Vrijednost zadanog izraza tada je jednaka: 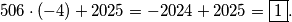 Kao rješenje upišite suprotan broj rješenja ovog zadatka.
Kao rješenje upišite suprotan broj rješenja ovog zadatka.
Izračunaj:
$$ 1+2-3-4+5+6-7-8+\dots +2025$$
\textit{Rješenje.} Uočimo pravilnost u ponavljanju pozitivnih i negativnih cijelih brojeva $\rightarrow$ dva pozitivna, dva negativna, dva pozitivna, dva negativna, itd. \\\\
Također, vrijedi da je $1-3=-2$, $2-4=-2$, $5-7=-2$, $6-8=-2$. Dakle, u toj jednoj grupi od 4 broja, prvi pozitivni i prvi negativni zbrojeni daju $-2$, isto kao i drugi pozitivni i drugi negativni. To znači da ta cijela grupa od $4$ broja daje sumu $-4$. Prikažimo zornije te grupe:
$$
\underbrace{1+2-3-4}_{-4}+\underbrace{5+6-7-8}_{-4}+\underbrace{9+10-11-12}_{-4}+\dots+2025.
$$
Moramo još dokučiti koliko takvih grupa ima. Uočimo da je posljednji broj svake grupe djeljiv s $4$, a budući da je $2024$ djeljiv s $4$, posljednja grupa izgleda ovako:
$$
\underbrace{2021+2022-2023-2024}_{-4}.
$$
Dakle, grupiramo prvih $2024$ brojeva u grupe po $4$. Takvih grupa ima $2024 : 4=506$.
\\\\
Vrijednost zadanog izraza tada je jednaka:
$$
506\cdot (-4)+2025=-2024+2025=\boxed1.
$$
Kao rješenje upišite suprotan broj rješenja ovog zadatka.
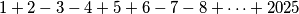 Rješenje. Uočimo pravilnost u ponavljanju pozitivnih i negativnih cijelih brojeva
Rješenje. Uočimo pravilnost u ponavljanju pozitivnih i negativnih cijelih brojeva 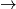 dva pozitivna, dva negativna, dva pozitivna, dva negativna, itd.
dva pozitivna, dva negativna, dva pozitivna, dva negativna, itd. 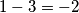 ,
, 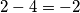 ,
, 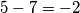 ,
, 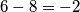 . Dakle, u toj jednoj grupi od 4 broja, prvi pozitivni i prvi negativni zbrojeni daju
. Dakle, u toj jednoj grupi od 4 broja, prvi pozitivni i prvi negativni zbrojeni daju  , isto kao i drugi pozitivni i drugi negativni. To znači da ta cijela grupa od
, isto kao i drugi pozitivni i drugi negativni. To znači da ta cijela grupa od  broja daje sumu
broja daje sumu 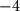 . Prikažimo zornije te grupe:
. Prikažimo zornije te grupe: 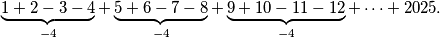 Moramo još dokučiti koliko takvih grupa ima. Uočimo da je posljednji broj svake grupe djeljiv s
Moramo još dokučiti koliko takvih grupa ima. Uočimo da je posljednji broj svake grupe djeljiv s  , a budući da je
, a budući da je 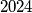 djeljiv s
djeljiv s  , posljednja grupa izgleda ovako:
, posljednja grupa izgleda ovako: 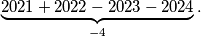 Dakle, grupiramo prvih
Dakle, grupiramo prvih 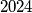 brojeva u grupe po
brojeva u grupe po  . Takvih grupa ima
. Takvih grupa ima 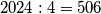 .
. 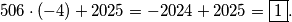 Kao rješenje upišite suprotan broj rješenja ovog zadatka.
Kao rješenje upišite suprotan broj rješenja ovog zadatka. 