a) Odredi sve 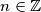 tako da je razlomak
tako da je razlomak 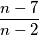 cijeli broj.
cijeli broj.
b) Odredi sve 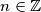 tako da je razlomak
tako da je razlomak 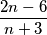 prirodni broj.
prirodni broj.
Rješenje. a) Kada bismo uspjeli transformirati ovaj razlomak u neki ljepši oblik, to bi nam puno pomoglo. Zapravo, kada bismo razdvojili ovaj razlomak u dva razlomka od kojih jedan možemo zapisati kao prirodan broj, to bi bilo sjajno. Stoga, zapišimo brojnik 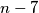 kao
kao 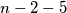 pa razdvojimo u dva razlomka:
pa razdvojimo u dva razlomka: 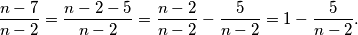 Ovo je puno bolje. Broj
Ovo je puno bolje. Broj  je sam po sebi cijeli broj, a cijeli izraz će biti jednak cijelom broju kada je
je sam po sebi cijeli broj, a cijeli izraz će biti jednak cijelom broju kada je 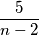 cijeli broj. Kada će to biti slučaj? To će biti kada
cijeli broj. Kada će to biti slučaj? To će biti kada  dijeli broj
dijeli broj  . Cijeli djelitelji broja
. Cijeli djelitelji broja  su
su 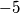 ,
,  ,
,  i
i  pa imamo:
pa imamo:

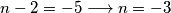 .
.
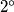
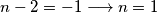 .
.
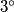
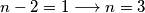 .
.
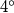
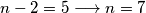 .
.
Konačno zapisujemo: 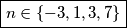 .
.
b) Možemo li ovdje napraviti nešto slično kao i u a)? Kada bismo u brojniku imali 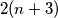 , to bi bilo sjajno, no
, to bi bilo sjajno, no 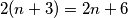 , a mi imamo
, a mi imamo 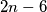 . Ipak, ako mi dodamo i oduzmemo
. Ipak, ako mi dodamo i oduzmemo  u brojniku, imamo traženi oblik. Redom to izgleda ovako:
u brojniku, imamo traženi oblik. Redom to izgleda ovako: 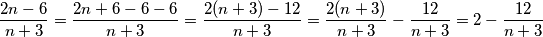 Uočimo kako konačni rezultat mora biti prirodni broj tako da razlomak
Uočimo kako konačni rezultat mora biti prirodni broj tako da razlomak 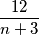 može poprimiti vrijednosti
može poprimiti vrijednosti  ,
,  ,
,  ,
, 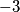 ,
, 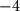 ,
, 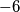 ili
ili 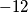 , a to je kad je
, a to je kad je 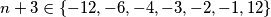 . Stoga je rješenje:
. Stoga je rješenje:  Kao rješenje upišite "razlomak"
Kao rješenje upišite "razlomak"
\textbf{a)} Odredi sve $n\in \mathbb{Z}$ tako da je razlomak $\dfrac{n-7}{n-2}$ cijeli broj. \\\\
\textbf{b)} Odredi sve $n\in \mathbb{Z}$ tako da je razlomak $\dfrac{2n-6}{n+3}$ prirodni broj. \\\\
\textit{Rješenje.} \textbf{a)} Kada bismo uspjeli transformirati ovaj razlomak u neki ljepši oblik, to bi nam puno pomoglo. Zapravo, kada bismo razdvojili ovaj razlomak u dva razlomka od kojih jedan možemo zapisati kao prirodan broj, to bi bilo sjajno. Stoga, zapišimo brojnik $n-7$ kao $n-2-5$ pa razdvojimo u dva razlomka:
$$
\dfrac{n-7}{n-2}=\dfrac{n-2-5}{n-2}=\dfrac{n-2}{n-2}-\dfrac{5}{n-2}=1-\dfrac{5}{n-2}.
$$
Ovo je puno bolje. Broj $1$ je sam po sebi cijeli broj, a cijeli izraz će biti jednak cijelom broju kada je $\dfrac{5}{n-2}$ cijeli broj. Kada će to biti slučaj? To će biti kada $n-2$ dijeli broj $5$. Cijeli djelitelji broja $5$ su $-5$, $-1$, $1$ i $5$ pa imamo: \\\\
$1^{\circ}$ $n-2=-5 \longrightarrow n=-3$. \\\\
$2^{\circ}$ $n-2=-1 \longrightarrow n=1$. \\\\
$3^{\circ}$ $n-2=1 \longrightarrow n=3$. \\\\
$4^{\circ}$ $n-2=5 \longrightarrow n=7$. \\\\
Konačno zapisujemo: $\boxed{n\in \{-3, 1, 3, 7\}}$. \\\\
\textbf{b)} Možemo li ovdje napraviti nešto slično kao i u \textbf{a)}? Kada bismo u brojniku imali $2(n+3)$, to bi bilo sjajno, no $2(n+3)=2n+6$, a mi imamo $2n-6$. Ipak, ako mi dodamo i oduzmemo $6$ u brojniku, imamo traženi oblik. Redom to izgleda ovako:
$$
\dfrac{2n-6}{n+3}=\dfrac{2n+6-6-6}{n+3}=\dfrac{2(n+3)-12}{n+3}=\dfrac{2(n+3)}{n+3}-\dfrac{12}{n+3}=2-\dfrac{12}{n+3}
$$
Uočimo kako konačni rezultat mora biti prirodni broj tako da razlomak $\dfrac{12}{n+3}$ može poprimiti vrijednosti $1$, $-1$, $-2$, $-3$, $-4$, $-6$ ili $-12$, a to je kad je $n+3\in\{-12, -6, -4, -3, -2, -1, 12\}$. Stoga je rješenje:
$$
\boxed{n\in \{-15, -9, -7, -6, -5, -4, 9\}}.
$$
Kao rješenje upišite "razlomak"
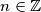 tako da je razlomak
tako da je razlomak 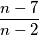 cijeli broj.
cijeli broj. 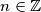 tako da je razlomak
tako da je razlomak 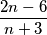 prirodni broj.
prirodni broj. 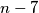 kao
kao 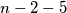 pa razdvojimo u dva razlomka:
pa razdvojimo u dva razlomka: 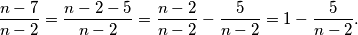 Ovo je puno bolje. Broj
Ovo je puno bolje. Broj  je sam po sebi cijeli broj, a cijeli izraz će biti jednak cijelom broju kada je
je sam po sebi cijeli broj, a cijeli izraz će biti jednak cijelom broju kada je 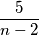 cijeli broj. Kada će to biti slučaj? To će biti kada
cijeli broj. Kada će to biti slučaj? To će biti kada  dijeli broj
dijeli broj  . Cijeli djelitelji broja
. Cijeli djelitelji broja  su
su 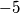 ,
,  ,
,  i
i  pa imamo:
pa imamo: 
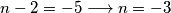 .
. 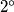
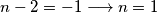 .
. 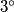
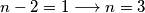 .
. 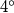
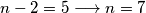 .
. 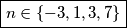 .
. 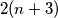 , to bi bilo sjajno, no
, to bi bilo sjajno, no 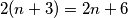 , a mi imamo
, a mi imamo 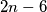 . Ipak, ako mi dodamo i oduzmemo
. Ipak, ako mi dodamo i oduzmemo  u brojniku, imamo traženi oblik. Redom to izgleda ovako:
u brojniku, imamo traženi oblik. Redom to izgleda ovako: 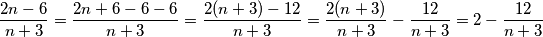 Uočimo kako konačni rezultat mora biti prirodni broj tako da razlomak
Uočimo kako konačni rezultat mora biti prirodni broj tako da razlomak 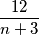 može poprimiti vrijednosti
može poprimiti vrijednosti  ,
,  ,
,  ,
, 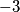 ,
, 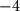 ,
, 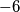 ili
ili 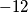 , a to je kad je
, a to je kad je 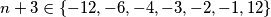 . Stoga je rješenje:
. Stoga je rješenje:  Kao rješenje upišite "razlomak"
Kao rješenje upišite "razlomak" 