Izračunaj: 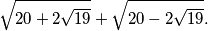 Rješenje. Evo i zadatka s korijenima. Za one koji se još nisu susretali s korijenima, iskažimo par važnih činjenica.
Rješenje. Evo i zadatka s korijenima. Za one koji se još nisu susretali s korijenima, iskažimo par važnih činjenica.
Drugi korijen iz nenegativnog broja  je nenegativni broj
je nenegativni broj  za koji vrijedi da je
za koji vrijedi da je 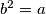 . Oznaka je
. Oznaka je 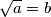 . Npr.
. Npr. 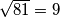 jer je
jer je 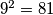 .
.
Vrijedi da je 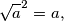 ali
ali 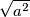 nije nužno jednak
nije nužno jednak  jer sada
jer sada  ne mora biti nenegativan broj. Npr.
ne mora biti nenegativan broj. Npr. 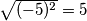 , a ne
, a ne 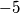 . Vrijedi:
. Vrijedi: 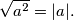 Vratimo se sada zadatku. Ove izraze ispod korijena možemo pojednostaviti tako da ih zapišemo kao kvadrate nečega. No, nije baš skroz jasno kako to napraviti.
Vratimo se sada zadatku. Ove izraze ispod korijena možemo pojednostaviti tako da ih zapišemo kao kvadrate nečega. No, nije baš skroz jasno kako to napraviti.
Ključ je u kvadratu zbroja i razlike. Vrijedi da je: 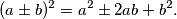 I sada, kada pogledamo ovaj
I sada, kada pogledamo ovaj 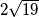 ispod oba velika korijena, malo nas možda podsjeća na
ispod oba velika korijena, malo nas možda podsjeća na 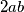 u gore navedenoj formuli. Čak bismo ga mogli i zapisati i kao
u gore navedenoj formuli. Čak bismo ga mogli i zapisati i kao 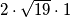 , no tada bismo ispod korijena morali imati i
, no tada bismo ispod korijena morali imati i 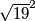 i
i 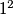 Međutim, mi to imamo! Vrijedi da je
Međutim, mi to imamo! Vrijedi da je 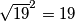 i
i 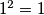 , a
, a 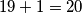 , upravo onaj broj koji je pod korijenom! Stoga, zapišimo sada
, upravo onaj broj koji je pod korijenom! Stoga, zapišimo sada  u "obrnutom smjeru" te izraze ispod korijena kao kvadrate zbroja/razlike (jednom rječju, binoma).
u "obrnutom smjeru" te izraze ispod korijena kao kvadrate zbroja/razlike (jednom rječju, binoma). 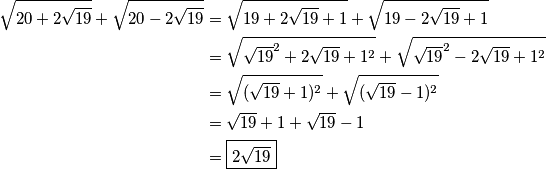 Kao rješenje upiši kvadrat rješenja ovog zadatka.
Kao rješenje upiši kvadrat rješenja ovog zadatka.
Izračunaj:
$$
\sqrt{20+2\sqrt{19}}+\sqrt{20-2\sqrt{19}}.
$$
\textit{Rješenje.} Evo i zadatka s korijenima. Za one koji se još nisu susretali s korijenima, iskažimo par važnih činjenica. \\\\
Drugi korijen iz nenegativnog broja $a$ je nenegativni broj $b$ za koji vrijedi da je $b^2=a$. Oznaka je $\sqrt{a}=b$. Npr. $\sqrt{81}=9$ jer je $9^2=81$.
\\\\
Vrijedi da je
$$
\sqrt{a}^2=a,
$$
ali $\sqrt{a^2}$ nije nužno jednak $a$ jer sada $a$ ne mora biti nenegativan broj. Npr. $\sqrt{(-5)^2}=5$, a ne $-5$. Vrijedi:
$$
\sqrt{a^2}=|a|.
$$
Vratimo se sada zadatku. Ove izraze ispod korijena možemo pojednostaviti tako da ih zapišemo kao kvadrate nečega. No, nije baš skroz jasno kako to napraviti.
\\\\
Ključ je u kvadratu zbroja i razlike. Vrijedi da je:
$$
(a\pm b)^2=a^2\pm 2ab+b^2.
$$
I sada, kada pogledamo ovaj $2\sqrt{19}$ ispod oba velika korijena, malo nas možda podsjeća na $2ab$ u gore navedenoj formuli. Čak bismo ga mogli i zapisati i kao $2\cdot \sqrt{19}\cdot 1$, no tada bismo ispod korijena morali imati i $\sqrt{19}^2$ i $1^2$ Međutim, mi to imamo! Vrijedi da je $\sqrt{19}^2=19$ i $1^2=1$, a $19+1=20$, upravo onaj broj koji je pod korijenom! Stoga, zapišimo sada $20$ u "obrnutom smjeru" te izraze ispod korijena kao kvadrate zbroja/razlike (jednom rječju, binoma).
\begin{align*}
\sqrt{20+2\sqrt{19}}+\sqrt{20-2\sqrt{19}}&=\sqrt{19+2\sqrt{19}+1}+\sqrt{19-2\sqrt{19}+1} \\
&=\sqrt{\sqrt{19}^2+2\sqrt{19}+1^2}+\sqrt{\sqrt{19}^2-2\sqrt{19}+1^2} \\
&=\sqrt{(\sqrt{19}+1)^2}+\sqrt{(\sqrt{19}-1)^2} \\
&=\sqrt{19}+1+\sqrt{19}-1 \\
&=\boxed{2\sqrt{19}}
\end{align*}
Kao rješenje upiši kvadrat rješenja ovog zadatka.
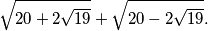 Rješenje. Evo i zadatka s korijenima. Za one koji se još nisu susretali s korijenima, iskažimo par važnih činjenica.
Rješenje. Evo i zadatka s korijenima. Za one koji se još nisu susretali s korijenima, iskažimo par važnih činjenica.  je nenegativni broj
je nenegativni broj  za koji vrijedi da je
za koji vrijedi da je 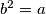 . Oznaka je
. Oznaka je 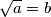 . Npr.
. Npr. 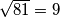 jer je
jer je 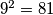 .
. 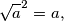 ali
ali 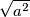 nije nužno jednak
nije nužno jednak  jer sada
jer sada  ne mora biti nenegativan broj. Npr.
ne mora biti nenegativan broj. Npr. 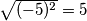 , a ne
, a ne 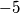 . Vrijedi:
. Vrijedi: 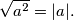 Vratimo se sada zadatku. Ove izraze ispod korijena možemo pojednostaviti tako da ih zapišemo kao kvadrate nečega. No, nije baš skroz jasno kako to napraviti.
Vratimo se sada zadatku. Ove izraze ispod korijena možemo pojednostaviti tako da ih zapišemo kao kvadrate nečega. No, nije baš skroz jasno kako to napraviti. 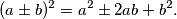 I sada, kada pogledamo ovaj
I sada, kada pogledamo ovaj 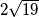 ispod oba velika korijena, malo nas možda podsjeća na
ispod oba velika korijena, malo nas možda podsjeća na 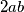 u gore navedenoj formuli. Čak bismo ga mogli i zapisati i kao
u gore navedenoj formuli. Čak bismo ga mogli i zapisati i kao 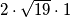 , no tada bismo ispod korijena morali imati i
, no tada bismo ispod korijena morali imati i 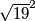 i
i 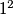 Međutim, mi to imamo! Vrijedi da je
Međutim, mi to imamo! Vrijedi da je 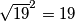 i
i 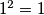 , a
, a 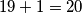 , upravo onaj broj koji je pod korijenom! Stoga, zapišimo sada
, upravo onaj broj koji je pod korijenom! Stoga, zapišimo sada  u "obrnutom smjeru" te izraze ispod korijena kao kvadrate zbroja/razlike (jednom rječju, binoma).
u "obrnutom smjeru" te izraze ispod korijena kao kvadrate zbroja/razlike (jednom rječju, binoma). 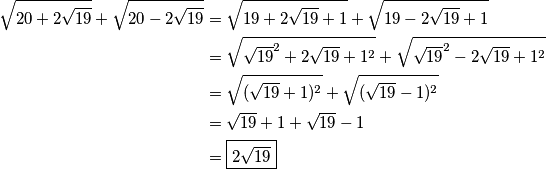 Kao rješenje upiši kvadrat rješenja ovog zadatka.
Kao rješenje upiši kvadrat rješenja ovog zadatka. 