MetaMath Junior '25

Djed je podijelio jabuke svojim unucima. Prvi je unuk dobio $1$ jabuku i $\dfrac{1}{5}$ ostatka, drugi je dobio $2$ jabuke i $\dfrac{1}{5}$ drugog ostatka, a treći $3$ jabuke i $\dfrac{1}{5}$ trećeg ostatka itd. Koliko je bilo jabuka, a koliko unuka ima djed? \\\\ \textit{Rješenje.} Imamo više nepoznatih veličina. Ipak, budući da se u uvjetima zadatka spominju ostatci jabuka, označimo sa $x$ broj jabuka. \\\\ Prvi je dobio $1$ jabuku i petinu ostatka, dakle $1+\dfrac{x-1}{5}$. 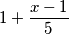Oduzeli smo jednu jabuku od ukupnog broja i sve podijelili sa 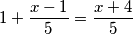$5$. $$ 1+\dfrac{x-1}{5}=\dfrac{x+4}{5} $$ Drugi je dobio $2$ jabuke i petinu ostatka. Sada ćemo ostatak dobiti tako da od $x$ oduzmemo ono što je dobio prvi unuk i ove $2$ jabuke koje dobiva drugi. 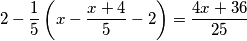Dakle: $$ 2-\dfrac{1}{5}\left(x-\dfrac{x+4}{5}-2\right)=\dfrac{4x+36}{25} $$ jabuka itd. \\\\ Svaki unuk je dobio isti broj jabuka pa možemo izjednačiti izraze za prvog i drugog unuka te riješiti jednadžbu: 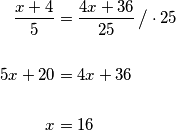\begin{align*} \dfrac{x+4}{5}&=\dfrac{4x+36}{25} \, \big \slash \cdot 25 \\\\ 5x+20&=4x+36 \\\\ x&=16 \end{align*} Dakle, bilo je 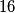$16$ jabuka što znači da je prvi unuk dobio 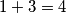$1+3=4$ jabuke. Kao rješenje upišite broj koliko unuka ima djed.