MetaMath Junior '25

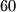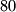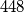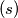Iz dvaju gradova istovremeno krenu jedan drugom ususret dva automobila, jedan brzinom $60$ km/h, drugi $80$ km/h. Ako su gradovi udaljeni $448$ km, nakon koliko će se vremena automobili susresti? \\\\ \textit{Rješenje.} Ovdje je najbitnije da znamo odnos između prosječne brzine, puta i vremena. Prosječnu brzinu ($v$) definiramo kao količnik prijeđenog puta $(s)$ u jedinici vremena ($t$), odnosno: $$ v=\dfrac{s}{t}. 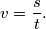$$ Uočimo kako je do trenutka susreta prošlo jednako vremena i prvom i drugom automobilu, stoga je strategija izraziti $t$ iz gornjeg izraza: $$ t=\dfrac{s}{v}. 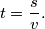$$ Brzine su nam poznate za oba automobila. Trebamo nekako još izraziti put. Znamo da je ukupna udaljenost gradova 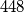$448$ km. Uvedimo sada nepoznanicu. Neka je $x$ put koji prijeđe prvi automobil do trenutka susreta. 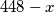Tada je $448-x$ put koji prijeđe drugi automobil. Uvrštavanjem u izraz za vrijeme 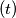$(t)$ dobivamo: 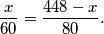$$ \dfrac{x}{60}=\dfrac{448-x}{80}. $$ Rješavanjem te jednadžbe dobiva se 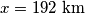$x=192\text{ km}$. Dakle, prvi automobil je, vozeći brzinom 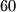$60$ km/h prešao 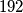$192$ km. Uvrstimo te podatke u izraz za vrijeme da otkrijemo koliko je vremena prošlo: 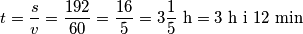$$ t=\dfrac{s}{v}=\dfrac{192}{60}=\dfrac{16}{5}=3\dfrac{1}{5}\text{ h}=3\text{ h i }12\text{ min} $$ Kao rješenje napišite dobiveno vrijeme u minutama.