Prvi tip zadataka riječima koji ćemo upoznati su zadaci podjele posla. Promotrimo o čemu je riječ na ovom primjeru s Županijskog natjecanja 2014. godine za 6. razred.
Zadatak: Dva radnika postavljaju parkete. Kada bi radio sam, prvi radnik bi posao završio za 4 dana. Zajedno bi posao završili za 3 dana. Međutim, nakon što su dva dana radili zajedno, prvi se radnik razbolio pa je drugi posao završio sam. Koliko dana je trajalo postavljanje parketa?
Rješenje: U ovakvim zadacima trik je uvijek isti: važno je pogledati koliko posla svaki od radnika obavi u jednoj jedinici vremena.
U našem slučaju, prvi radnik u jedan dan odradi  posla.
posla.
Ne znamo koliko posla drugi radnik odradi sam u jedan dan, no znamo da prvi i drugi radnik u jedan dan zajedno odrade  posla.
posla.
Sada jednostavno dobijemo koliko posla obavi drugi radnik u jednom danu tako da od onoga što obave zajedno oduzmemo ono što obavi prvi radnik: 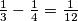 . Dakle, u jednom danu drugi radnik sam obavi
. Dakle, u jednom danu drugi radnik sam obavi 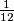 posla.
posla.
Sada kada imamo sve elemente, promotrimo što se događa po danima:
Prvi i drugi dan oba radnika rade zajedno i obave 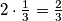 posla.
posla.
Ostale dane potrebno je obaviti 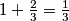 posla. Ostalih
posla. Ostalih  dana drugi radnik radio je sam. Ukupno je obavio
dana drugi radnik radio je sam. Ukupno je obavio 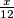 posla. To je zapravo ona preostala trećina posla, stoga lako računamo
posla. To je zapravo ona preostala trećina posla, stoga lako računamo  :
: 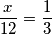
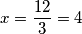
Dakle, drugi radnik radio je sam  dana. Zajedno s ona prva
dana. Zajedno s ona prva  dana, postavljanje parketa trajalo je
dana, postavljanje parketa trajalo je  dana.
dana.
Na prvi pogled čini se da je jadni drugi radnik radio puno više nego prvi. Ipak je on bio na poslu 6 dana, a prvi samo 2! No, izračunamo li zapravo koliko je posla obavio prvi radnik, dobijemo da je on obavio 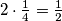 posla. Dakle, prvi dojam nas je prevario. Podjela posla je ipak bila sasvim podjednaka!
posla. Dakle, prvi dojam nas je prevario. Podjela posla je ipak bila sasvim podjednaka!
-----------------------------------------
Kao rješenje upišite broj radnih dana u tjednu.
Prvi tip zadataka riječima koji ćemo upoznati su zadaci podjele posla. Promotrimo o čemu je riječ na ovom primjeru s Županijskog natjecanja 2014. godine za 6. razred.
\textbf{Zadatak: }Dva radnika postavljaju parkete. Kada bi radio sam, prvi radnik bi posao završio za 4 dana. Zajedno bi posao završili za 3 dana. Međutim, nakon što su dva dana radili zajedno, prvi se radnik razbolio pa je drugi posao završio sam. Koliko dana je trajalo postavljanje parketa?
\textbf{Rješenje:}
U ovakvim zadacima trik je uvijek isti: važno je pogledati \textbf{koliko posla svaki od radnika obavi u jednoj jedinici vremena.}
U našem slučaju, prvi radnik u jedan dan odradi $\frac 14$ posla.
\begin{center}
\includegraphics{p11.png}
\end{center}
Ne znamo koliko posla drugi radnik odradi sam u jedan dan, no znamo da prvi i drugi radnik u jedan dan zajedno odrade $\frac 13$ posla.
\begin{center}
\includegraphics{p12.png}
\end{center}
Sada jednostavno dobijemo koliko posla obavi drugi radnik u jednom danu tako da od onoga što obave zajedno oduzmemo ono što obavi prvi radnik: $\frac 13 - \frac 14 = \frac 1{12}$. Dakle, u jednom danu drugi radnik sam obavi $\frac 1{12}$ posla.
\begin{center}
\includegraphics{p15.png}
\end{center}
Sada kada imamo sve elemente, promotrimo što se događa po danima:
Prvi i drugi dan oba radnika rade zajedno i obave $2\cdot \frac 13 = \frac 23$ posla.
\begin{center}
\includegraphics{p13.png}
\end{center}
Ostale dane potrebno je obaviti $1 + \frac 23 = \frac 13$ posla.
Ostalih $x$ dana drugi radnik radio je sam. Ukupno je obavio $\frac x{12}$ posla. To je zapravo ona preostala trećina posla, stoga lako računamo $x$:
$$\frac x{12} = \frac 13$$
$$x = \frac{12}3 = 4$$
Dakle, drugi radnik radio je sam $4$ dana. Zajedno s ona prva $2$ dana, postavljanje parketa trajalo je $6$ dana.
\begin{center}
\includegraphics{p16.png}
\end{center}
Na prvi pogled čini se da je jadni drugi radnik radio puno više nego prvi. Ipak je on bio na poslu 6 dana, a prvi samo 2! No, izračunamo li zapravo koliko je posla obavio prvi radnik, dobijemo da je on obavio $2\cdot \frac 14 = \frac 12$ posla. Dakle, prvi dojam nas je prevario. Podjela posla je ipak bila sasvim podjednaka!
-----------------------------------------\\
Kao rješenje upišite broj radnih dana u tjednu.
 posla.
posla. 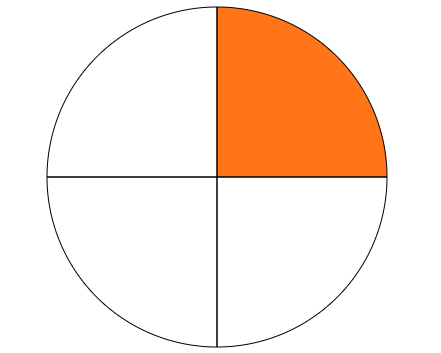
 posla.
posla. 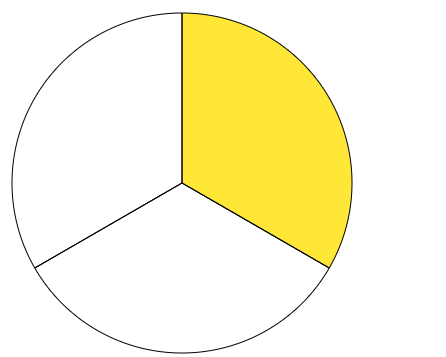
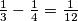 . Dakle, u jednom danu drugi radnik sam obavi
. Dakle, u jednom danu drugi radnik sam obavi 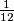 posla.
posla.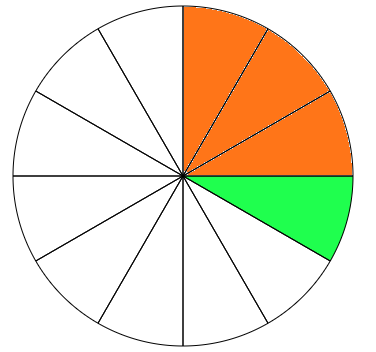
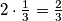 posla.
posla. 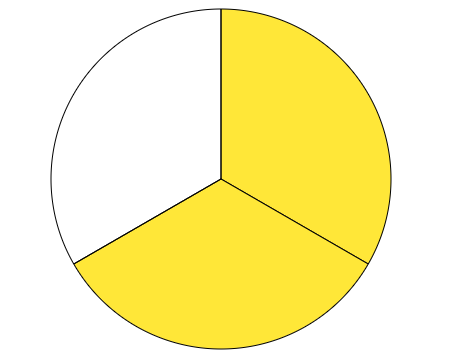
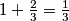 posla. Ostalih
posla. Ostalih  dana drugi radnik radio je sam. Ukupno je obavio
dana drugi radnik radio je sam. Ukupno je obavio 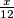 posla. To je zapravo ona preostala trećina posla, stoga lako računamo
posla. To je zapravo ona preostala trećina posla, stoga lako računamo  :
: 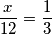
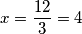
 dana. Zajedno s ona prva
dana. Zajedno s ona prva  dana, postavljanje parketa trajalo je
dana, postavljanje parketa trajalo je  dana.
dana. 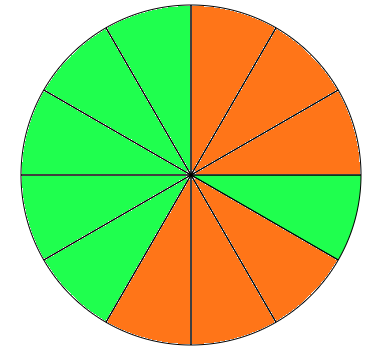
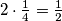 posla. Dakle, prvi dojam nas je prevario. Podjela posla je ipak bila sasvim podjednaka!
posla. Dakle, prvi dojam nas je prevario. Podjela posla je ipak bila sasvim podjednaka!