Zadatak. Odredi najmanji troznamenkasti prirodni broj koji pri dijeljenju s  ,
,  i
i  daje ostatak
daje ostatak  .
.
------------------------------------------------------------------------------------------------------------------------------------------------
Rješenje. Koristimo li navedeni zapis dijeljenja traženog broja  s brojevima
s brojevima  ,
,  i
i  , dobijemo:
, dobijemo: 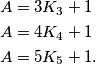 Brojevi
Brojevi 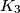 ,
, 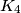 i
i 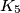 su količnici pri dijeljenju broja
su količnici pri dijeljenju broja  redom s
redom s  ,
,  i
i  ; ostatak je u svakom dijeljenju je
; ostatak je u svakom dijeljenju je  . Ono što je sada sjajno je da odavde možemo primijetiti da ako oduzmemo
. Ono što je sada sjajno je da odavde možemo primijetiti da ako oduzmemo  s obje strane sve tri jednakosti, dobivamo:
s obje strane sve tri jednakosti, dobivamo: 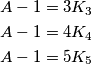 Ovo je jako lijepo, zato što nam govori da je broj
Ovo je jako lijepo, zato što nam govori da je broj  umanjen za
umanjen za  djeljiv s
djeljiv s  ,
,  i
i  . Tada je sigurno djeljiv i sa zajedničkim višekratnicima od
. Tada je sigurno djeljiv i sa zajedničkim višekratnicima od  ,
,  i
i  , tj. s
, tj. s 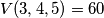 (ponovit ćemo poslije malo detaljnije svojstva najmanjeg zajedničkog višekratnika). Dakle, naš plan je naći najmanji troznamenkasti višekratnik od
(ponovit ćemo poslije malo detaljnije svojstva najmanjeg zajedničkog višekratnika). Dakle, naš plan je naći najmanji troznamenkasti višekratnik od 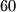 i uvećati ga za
i uvećati ga za  .
.
Upiši konačno rješenje!
\textbf{Zadatak.} Odredi najmanji troznamenkasti prirodni broj koji pri dijeljenju s $3$, $4$ i $5$ daje ostatak $1$.
------------------------------------------------------------------------------------------------------------------------------------------------
\textbf{Rješenje.} Koristimo li navedeni zapis dijeljenja traženog broja $A$ s brojevima $3$, $4$ i $5$, dobijemo:
\begin{align*}
A&=3K_3+1 \\
A&=4K_4+1 \\
A&=5K_5+1 \text.
\end{align*}
Brojevi $K_3$, $K_4$ i $K_5$ su količnici pri dijeljenju broja $A$ redom s $3$, $4$ i $5$; ostatak je u svakom dijeljenju je $1$. Ono što je sada sjajno je da odavde možemo primijetiti da ako oduzmemo $1$ s obje strane sve tri jednakosti, dobivamo:
\begin{align*}
A-1&=3K_3 \\
A-1&=4K_4 \\
A-1&=5K_5
\end{align*}
Ovo je jako lijepo, zato što nam govori da je broj $A$ umanjen za $1$ \textbf{djeljiv} s $3$, $4$ i $5$. Tada je sigurno djeljiv i sa zajedničkim višekratnicima od $3$, $4$ i $5$, tj.~s $V(3, 4, 5)=60$ (ponovit ćemo poslije malo detaljnije svojstva najmanjeg zajedničkog višekratnika). Dakle, naš plan je naći najmanji troznamenkasti višekratnik od $60$ i uvećati ga za $1$.
Upiši konačno rješenje!
 ,
,  i
i  daje ostatak
daje ostatak  .
. s brojevima
s brojevima  ,
,  i
i  , dobijemo:
, dobijemo: 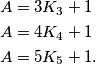 Brojevi
Brojevi 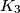 ,
, 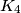 i
i 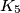 su količnici pri dijeljenju broja
su količnici pri dijeljenju broja  redom s
redom s  ,
,  i
i  ; ostatak je u svakom dijeljenju je
; ostatak je u svakom dijeljenju je  . Ono što je sada sjajno je da odavde možemo primijetiti da ako oduzmemo
. Ono što je sada sjajno je da odavde možemo primijetiti da ako oduzmemo  s obje strane sve tri jednakosti, dobivamo:
s obje strane sve tri jednakosti, dobivamo: 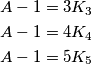 Ovo je jako lijepo, zato što nam govori da je broj
Ovo je jako lijepo, zato što nam govori da je broj  umanjen za
umanjen za  djeljiv s
djeljiv s  ,
,  i
i  . Tada je sigurno djeljiv i sa zajedničkim višekratnicima od
. Tada je sigurno djeljiv i sa zajedničkim višekratnicima od  ,
,  i
i  , tj. s
, tj. s 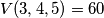 (ponovit ćemo poslije malo detaljnije svojstva najmanjeg zajedničkog višekratnika). Dakle, naš plan je naći najmanji troznamenkasti višekratnik od
(ponovit ćemo poslije malo detaljnije svojstva najmanjeg zajedničkog višekratnika). Dakle, naš plan je naći najmanji troznamenkasti višekratnik od 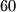 i uvećati ga za
i uvećati ga za  .
.