Ostatci - 3
Već u ovom prvom primjeru susreli smo se s pojmom najmanjeg zajedničkog višekratnika nekoliko prirodnih brojeva. To je jednostavno najmanji prirodni broj koji je djeljiv sa svim navedenim brojevima. Sigurni smo da znate proceduru kojom se određuje: rastavimo svaki broj na proste faktore i pomnožimo sve dobivene proste faktore, s tim da za svaki gledamo koliko najviše puta se ponavlja u nekom od brojeva i toliko puta ga množimo. Slična priča je i za određivanje najvećeg zajedničkog djelitelja nekoliko prirodnih brojeva -- to je najveći prirodni broj koji dijeli sve te brojeve.
Možda već znate, a inače ćete sad saznati, da za ova dva broja vrijedi sljedeće lijepo svojstvo. Neka su brojevi označeni s  i
i  , njihov najmanji zajednički višekratnik s
, njihov najmanji zajednički višekratnik s 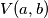 , a najveći zajednički djelitelj s
, a najveći zajednički djelitelj s 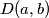 . Tada vrijedi:
. Tada vrijedi: 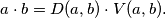
Kao rješenje upiši koliko iznosi umnožak dva broja čiji najveći zajednički djelitelj je  , a najmanji zajednički višekratnik
, a najmanji zajednički višekratnik 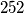 .
.
