Zadatak. Odredi prirodne brojeve  i
i  ,
, 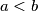 za koje vrijedi:
za koje vrijedi: 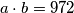 , i
, i 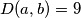 .
.
---------------------------------------------------------------------------------------------------------------
Rješenje. Budući da je najveći zajednički djelitelj tih brojeva  , oni se mogu zapisati kao
, oni se mogu zapisati kao 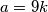 ,
, 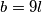 , gdje su
, gdje su  i
i  prirodni brojevi.
prirodni brojevi.
Budući da je 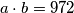 , vrijedi
, vrijedi 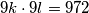 i nakon dijeljenja s
i nakon dijeljenja s 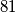 imamo
imamo 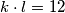 . Imamo
. Imamo  mogućnosti:
mogućnosti:
Prva je da je 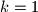 ,
, 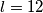 . Tada su
. Tada su  i
i  jednaki:
jednaki: 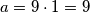 ,
, 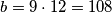 . Stoga, jedno rješenje je
. Stoga, jedno rješenje je 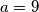 ,
, 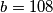 .
.
Druga je da je 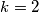 ,
, 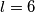 . Tada su
. Tada su  i
i  jednaki:
jednaki: 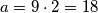 ,
, 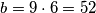 . No, ovo nije rješenje jer je
. No, ovo nije rješenje jer je 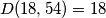 , a ne
, a ne  kao što je zadano u zadatku.
kao što je zadano u zadatku.
Treća je da je 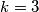 ,
, 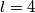 . Tada su
. Tada su  i
i  jednaki:
jednaki: 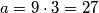 ,
, 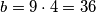 . Stoga, drugo rješenje je
. Stoga, drugo rješenje je 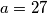 ,
, 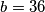 .
.
Kao rješenje upiši 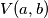 .
.
\textbf{Zadatak.} Odredi prirodne brojeve $a$ i $b$, $a<b$ za koje vrijedi: $a\cdot b=972$, i $D(a, b)=9$.
---------------------------------------------------------------------------------------------------------------
\textbf{Rješenje.} Budući da je najveći zajednički djelitelj tih brojeva $9$, oni se mogu zapisati kao $a=9k$, $b=9l$, gdje su $k$ i $l$ prirodni brojevi. \\\\
Budući da je $a\cdot b=972$, vrijedi $9k\cdot 9l=972$ i nakon dijeljenja s $81$ imamo $k\cdot l=12$. Imamo $3$ mogućnosti:
\\\\
Prva je da je $k=1$, $l=12$. Tada su $a$ i $b$ jednaki: $a=9\cdot 1=9$, $b=9\cdot 12=108$. Stoga, jedno rješenje je $a=9$, $b=108$.
\\\\
Druga je da je $k=2$, $l=6$. Tada su $a$ i $b$ jednaki: $a=9\cdot 2=18$, $b=9\cdot 6=52$. No, ovo nije rješenje jer je $D(18, 54)=18$, a ne $9$ kao što je zadano u zadatku.
\\\\
Treća je da je $k=3$, $l=4$. Tada su $a$ i $b$ jednaki: $a=9\cdot 3=27$, $b=9\cdot 4=36$. Stoga, drugo rješenje je $a=27$, $b=36$.\\\\
Kao rješenje upiši $V(a, b)$.
 i
i  ,
, 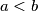 za koje vrijedi:
za koje vrijedi: 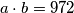 , i
, i 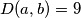 .
. , oni se mogu zapisati kao
, oni se mogu zapisati kao 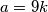 ,
, 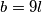 , gdje su
, gdje su  i
i  prirodni brojevi.
prirodni brojevi. 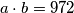 , vrijedi
, vrijedi 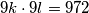 i nakon dijeljenja s
i nakon dijeljenja s 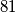 imamo
imamo 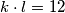 . Imamo
. Imamo  mogućnosti:
mogućnosti: 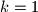 ,
, 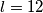 . Tada su
. Tada su  i
i  jednaki:
jednaki: 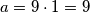 ,
, 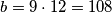 . Stoga, jedno rješenje je
. Stoga, jedno rješenje je 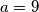 ,
, 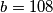 .
. 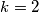 ,
, 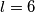 . Tada su
. Tada su  i
i  jednaki:
jednaki: 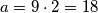 ,
, 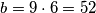 . No, ovo nije rješenje jer je
. No, ovo nije rješenje jer je 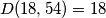 , a ne
, a ne  kao što je zadano u zadatku.
kao što je zadano u zadatku. 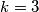 ,
, 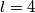 . Tada su
. Tada su  i
i  jednaki:
jednaki: 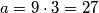 ,
, 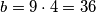 . Stoga, drugo rješenje je
. Stoga, drugo rješenje je 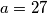 ,
, 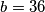 .
.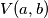 .
. 