Zadatak. Odredi dva prosta broja tako da je i njihov zbroj i njihova razlika također prost broj.
--------------------------------------------------------------------------------------------------------------
Rješenje. Budući da je zbroj dvaju prostih brojeva prosti broj, mora vrijediti da je jedan od tih brojeva  , jedini prosti broj, jer bi u suprotnom imali zbroj dva neparna broja što je paran broj koji nije prost.
, jedini prosti broj, jer bi u suprotnom imali zbroj dva neparna broja što je paran broj koji nije prost.
Označimo drugi prosti broj s  te je
te je 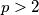 . Zbroj i razlika prostih brojeva iz zadatka su tada
. Zbroj i razlika prostih brojeva iz zadatka su tada 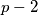 i
i 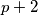 te oni moraju biti prosti brojevi.
te oni moraju biti prosti brojevi.
Dakle, 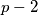 ,
,  i
i 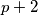 su tri uzastopna neparna prosta broja i među njima je točno jedan djeljiv s
su tri uzastopna neparna prosta broja i među njima je točno jedan djeljiv s  , a budući da su to prosti brojevi, taj broj mora biti točno
, a budući da su to prosti brojevi, taj broj mora biti točno  .
.
Sigurno 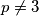 jer je tada
jer je tada 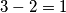 , što nije prost broj. Slično,
, što nije prost broj. Slično, 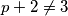 jer je tada
jer je tada 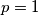 . Zato vrijedi da je
. Zato vrijedi da je 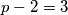 , tj.
, tj. 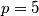 .
.
Traženi brojevi su  i
i  . Upiši ih,odvojene zarezima.
. Upiši ih,odvojene zarezima.
\textbf{Zadatak.} Odredi dva prosta broja tako da je i njihov zbroj i njihova razlika također prost broj.
--------------------------------------------------------------------------------------------------------------
\textbf{Rješenje.} Budući da je zbroj dvaju prostih brojeva prosti broj, mora vrijediti da je jedan od tih brojeva $2$, jedini prosti broj, jer bi u suprotnom imali zbroj dva neparna broja što je paran broj koji nije prost.
\\\\
Označimo drugi prosti broj s $p$ te je $p>2$. Zbroj i razlika prostih brojeva iz zadatka su tada $p-2$ i $p+2$ te oni moraju biti prosti brojevi.
\\\\
Dakle, $p-2$, $p$ i $p+2$ su tri uzastopna neparna prosta broja i među njima je točno jedan djeljiv s $3$, a budući da su to prosti brojevi, taj broj mora biti točno $3$.
\\\\
Sigurno $p\neq 3$ jer je tada $3-2=1$, što nije prost broj. Slično, $p+2\neq 3$ jer je tada $p=1$. Zato vrijedi da je $p-2=3$, tj. $p=5$. \\\\
Traženi brojevi su $2$ i $5$. Upiši ih,odvojene zarezima.
 , jedini prosti broj, jer bi u suprotnom imali zbroj dva neparna broja što je paran broj koji nije prost.
, jedini prosti broj, jer bi u suprotnom imali zbroj dva neparna broja što je paran broj koji nije prost.  te je
te je 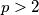 . Zbroj i razlika prostih brojeva iz zadatka su tada
. Zbroj i razlika prostih brojeva iz zadatka su tada 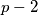 i
i 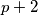 te oni moraju biti prosti brojevi.
te oni moraju biti prosti brojevi. 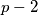 ,
,  i
i 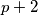 su tri uzastopna neparna prosta broja i među njima je točno jedan djeljiv s
su tri uzastopna neparna prosta broja i među njima je točno jedan djeljiv s  , a budući da su to prosti brojevi, taj broj mora biti točno
, a budući da su to prosti brojevi, taj broj mora biti točno  .
. 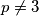 jer je tada
jer je tada 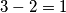 , što nije prost broj. Slično,
, što nije prost broj. Slično, 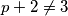 jer je tada
jer je tada 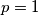 . Zato vrijedi da je
. Zato vrijedi da je 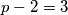 , tj.
, tj. 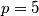 .
.  i
i  . Upiši ih,odvojene zarezima.
. Upiši ih,odvojene zarezima. 