Zadatak. Dokaži da svaki prosti broj veći od  ima oblik
ima oblik 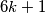 ili
ili 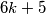 , pri čemu je
, pri čemu je  prirodan broj.
prirodan broj.
--------------------------------------------------------------------------------------------------------------------------------------------
Rješenje. Očito, brojevi djeljivi s  imaju oblik
imaju oblik 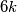 , a oni nisu prosti. Brojevi oblika
, a oni nisu prosti. Brojevi oblika 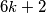 su djeljivi s
su djeljivi s  , brojevi oblika
, brojevi oblika 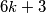 su djeljivi s
su djeljivi s  , a brojevi oblika
, a brojevi oblika 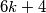 su djeljivi s
su djeljivi s  . Dakle, brojevi oblika
. Dakle, brojevi oblika 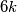 ,
, 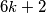 ,
, 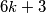 i
i 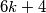 nisu prosti brojevi, tj. da bi broj bio prost, mora biti oblika
nisu prosti brojevi, tj. da bi broj bio prost, mora biti oblika 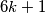 ili
ili 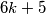 čime je dokaz gotov.
čime je dokaz gotov.
Napominjemo da to ne znači da su brojevi oblika 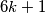 ili
ili 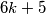 nužno prosti brojevi.
nužno prosti brojevi.
Također, kraće možemo reći da su prosti brojevi oblika 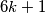 ili
ili 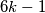 , tj.
, tj. 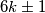 .
.
Kao rješenje upiši jedini prost broj između 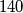 i
i 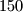 .
.
\textbf{Zadatak.} Dokaži da svaki prosti broj veći od $3$ ima oblik $6k+1$ ili $6k+5$, pri čemu je $k$ prirodan broj.
--------------------------------------------------------------------------------------------------------------------------------------------
\textbf{Rješenje.} Očito, brojevi djeljivi s $6$ imaju oblik $6k$, a oni nisu prosti. Brojevi oblika $6k+2$ su djeljivi s $2$, brojevi oblika $6k+3$ su djeljivi s $3$, a brojevi oblika $6k+4$ su djeljivi s $2$. Dakle, brojevi oblika $6k$, $6k+2$, $6k+3$ i $6k+4$ nisu prosti brojevi, tj. da bi broj bio prost, mora biti oblika $6k+1$ ili $6k+5$ čime je dokaz gotov.
\\\\
Napominjemo da to ne znači da su brojevi oblika $6k+1$ ili $6k+5$ nužno prosti brojevi.
\\\\
Također, kraće možemo reći da su prosti brojevi oblika $6k+1$ ili $6k-1$, tj. $6k \pm 1$.
Kao rješenje upiši jedini prost broj između $140$ i $150$.
 ima oblik
ima oblik 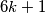 ili
ili 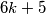 , pri čemu je
, pri čemu je  prirodan broj.
prirodan broj. imaju oblik
imaju oblik 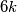 , a oni nisu prosti. Brojevi oblika
, a oni nisu prosti. Brojevi oblika 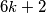 su djeljivi s
su djeljivi s  , brojevi oblika
, brojevi oblika 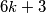 su djeljivi s
su djeljivi s  , a brojevi oblika
, a brojevi oblika 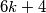 su djeljivi s
su djeljivi s  . Dakle, brojevi oblika
. Dakle, brojevi oblika 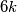 ,
, 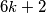 ,
, 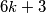 i
i 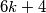 nisu prosti brojevi, tj. da bi broj bio prost, mora biti oblika
nisu prosti brojevi, tj. da bi broj bio prost, mora biti oblika 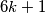 ili
ili 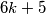 čime je dokaz gotov.
čime je dokaz gotov. 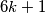 ili
ili 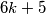 nužno prosti brojevi.
nužno prosti brojevi. 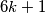 ili
ili 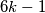 , tj.
, tj. 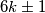 .
.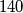 i
i 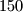 .
. 