MetaMath Junior '25

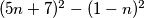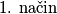
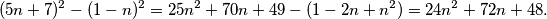
Dokaži da je za svaki cijeli broj $n$ broj $(5n+7)^2-(1-n)^2$ djeljiv s 48. \\\\ \textit{Rješenje.} Riješit ćemo zadatak na dva načina. \\\\ $\text{1. način}$ Kvadrirajmo izraze u zagradama i pojednostavnimo izraz: $$ (5n+7)^2-(1-n)^2=25n^2+70n+49-(1-2n+n^2)=24n^2+72n+48. $$ Zašto je ovaj izraz djeljiv s 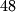$48$? Naravno, ideja je da se izluči zajednički faktor, ali tada dobivamo: $$ 24(n^2+3n+2). 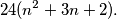$$ Ovo je sigurno djeljivo s 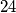$24$, no kako pokazati djeljivost s 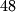$48$? "Trik" je u tome da član 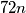$72n$ zapišemo drugačije, kao 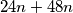$24n+48n$. Tada izlučujemo zajednički faktor u "parovima", u prva dva člana i u druga dva. $$ 24n^2+72n+48=24n^2+24n+48n+48=24n(n+1)+48(n+1). 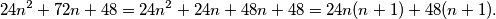$$ Drugi pribrojnik, 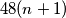$48(n+1)$, je očito djeljiv s 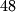$48$. U izrazu 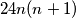$24n(n+1)$ imamo umnožak dva uzastopna cijela broja, a među njima je sigurno je jedan broj paran pa i taj umnožak mora biti paran. 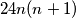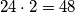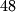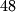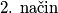Stoga je $24n(n+1)$ sigurno djeljiv s $24\cdot 2=48$, a cijeli izraz je djeljiv s $48$ kao zbroj dvaju izraza djeljivih s $48$. $\text{2. 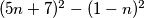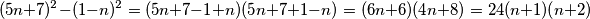način}$ Prepoznajmo razliku kvadrata u izrazu $(5n+7)^2-(1-n)^2$ te pojednostavnimo: $$(5n+7)^2-(1-n)^2=(5n+7-1+n)(5n+7+1-n)=(6n+6)(4n+8)=24(n+1)(n+2)$$ Umnožak 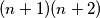$(n+1)(n+2)$ mora biti paran broj kao umnožak dva uzastopna broja pa cijeli izraz mora biti djeljiv s 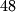$48$. Kao rješenje upišite broj prirodnih djelitelja broja 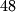$48$.