MetaMath Junior '25

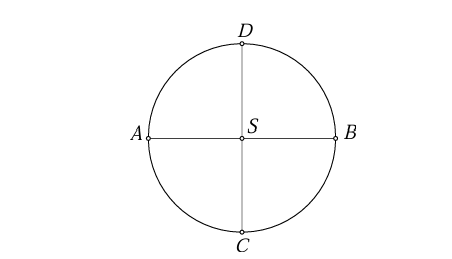
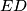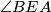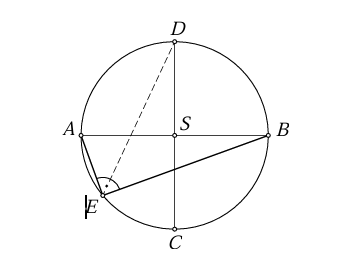
Promotrimo primjenu na zadatku. \\ \textbf{Zadatak:}\\ Dana su dva okomita promjera kao na slici. Na luku $AC$ odabrana je proizvoljna točka $E$. Dokažite da je $ED$ simetrala kuta $\angle BEA$. \begin{center} \includegraphics{obodni1.png} \end{center} \textbf{Rješenje:} \begin{center} \includegraphics{obodni2.png} \end{center} Iz Talesovog poučka slijedi: 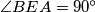$\angle BEA = 90^\circ$ (jer je $\overline{AB}$ promjer). Kut 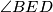$\angle BED$ je obodni kut nad lukom $BD$, a pripadni središnji kut je 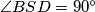$\angle BSD = 90^\circ$. Prema teoremu o obodnom i središnjem kutu imamo: 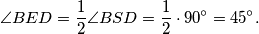\[ \angle BED = \frac{1}{2}\angle BSD = \frac{1}{2}\cdot 90^\circ = 45^\circ. \] Dakle, 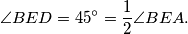\[ \angle BED = 45^\circ = \frac{1}{2}\angle BEA. \] Time je dokazano da je 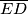$\overline{ED}$ simetrala kuta 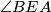$\angle BEA$. Kao rješenje zadatka upišite površinu pravokutnog trokuta koji ima katete duljina 3 i 4.