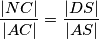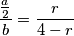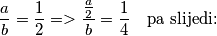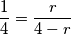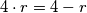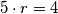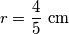Promotrimo primjer zadatka s Državnog natjecanja 2007. za sedme razrede.
Zadatak:
Duljina kraka jednakokračnog trokuta dvostruko je veća od duljine osnovice.
Izračunaj polumjer trokutu upisane kružnice ako je duljina visine na osnovicu 
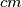 .
.
Rješenje:
Kao rješenje upišite rješenje ovog zadatka zaokruženo na jednu decimalu.
Promotrimo primjer zadatka s Državnog natjecanja 2007. za sedme razrede.
\textbf{Zadatak:}\\
Duljina kraka jednakokračnog trokuta dvostruko je veća od duljine osnovice.\\
Izračunaj polumjer trokutu upisane kružnice ako je duljina visine na osnovicu $4$ $cm$.\\
\textbf{Rješenje:}\\
\begin{center}
\includegraphics{upisane1.png}
\end{center}
\begin{center}
$ |AN| = 4 $ $cm$
$|SN| = |SD| = r $\\ \\
$=> |AS| = 4 - r$
$\Delta ANC$ i $\Delta ADS$ su slični jer su pravokutni sa zajedničkim kutom $\angle NAC$ pa imamo
\[
\frac{|NC|}{|AC|} = \frac{|DS|}{|AS|}
\]
\[
\frac{\frac{a}{2}}{b}= \frac{r}{4 - r}
\]
Ali, još znamo da vrijedi
\[\frac{a}{b} = \frac{1}{2} => \frac{\frac{a}{2}}{b}=\frac{1}{4} \quad \text{pa slijedi:}
\]
\[
\frac{1}{4} = \frac{r}{4 - r}
\]
\[
4 \cdot r = 4 - r
\]
\[
5 \cdot r = 4
\]
\[
r = \frac{4}{5}\ \text{cm}
\]
\end{center}
Kao rješenje upišite rješenje ovog zadatka zaokruženo na jednu decimalu.

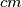 .
.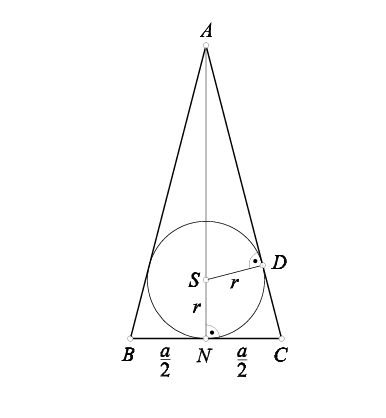
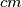
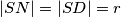
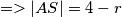
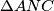 i
i 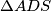 su slični jer su pravokutni sa zajedničkim kutom
su slični jer su pravokutni sa zajedničkim kutom 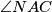 pa imamo
pa imamo