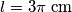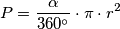Promotrimo svojstva tangenti na kružnicu na primjeru četvrtog zadatka sa Školskog natjecanja iz 2017. u kategoriji osmih razreda.
Zadatak:
Iz točke 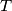 povučene su tangente na kružnicu polumjera
povučene su tangente na kružnicu polumjera 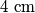 .
.
Izračunaj duljinu kružnog luka te kružnice koji se vidi iz točke 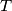 , ako tangente zatvaraju kut od
, ako tangente zatvaraju kut od 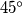 .
.
Rješenje:
Tangente su okomite na polumjere 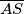 i
i 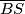 . Ta je činjenica jedna od najvjerojatnijih stvari koja će vam trebati čim se u zadatku spominju tangente pa uvijek prvo pokušajte vidjeti postoji li neka korisna dužina za koju bi se moglo primijeniti to pravilo, a da bi mogla ujedno još nečemu koristiti u zadatku.
. Ta je činjenica jedna od najvjerojatnijih stvari koja će vam trebati čim se u zadatku spominju tangente pa uvijek prvo pokušajte vidjeti postoji li neka korisna dužina za koju bi se moglo primijeniti to pravilo, a da bi mogla ujedno još nečemu koristiti u zadatku.
Kutovi 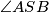 i
i 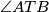 su kutovi s okomitim kracima, od kojih je jedan šiljasti, a drugi tupi, pa vrijedi:
su kutovi s okomitim kracima, od kojih je jedan šiljasti, a drugi tupi, pa vrijedi: 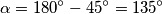
Duljinu kružnog luka računamo po formuli: 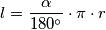 Uvrštavanjem vrijednosti:
Uvrštavanjem vrijednosti: 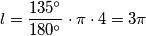
Duljina kružnog luka koji se vidi iz točke 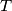 je:
je: 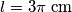
Kako se već koristi formula za duljinu kružnog luka, nevezano uz zadatak, ali korisno u tipovima zadataka gdje se traže nekakvi udjeli ili omjeri površina, površina kružnog isječka radijusa r i kuta alfa omeđenog u zadatku spomenutim kružnim lukom, dana je sličnom formulom kao i duljina luka: 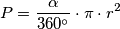
Kao rješenje ovog zadatka upišite, zaokružen na jednu decimalu, iznos površine koji bi imao kružni isječak omeđen kružnim lukom iz zadatka - dakle, radijusa kružnice 4 cm i kuta 135 stupnjeva.
Promotrimo svojstva tangenti na kružnicu na primjeru četvrtog zadatka sa Školskog natjecanja iz 2017. u kategoriji osmih razreda.
\textbf{Zadatak:}
Iz točke \(T\) povučene su tangente na kružnicu polumjera \(4 \ \text{cm}\).
Izračunaj duljinu kružnog luka te kružnice koji se vidi iz točke \(T\), ako tangente zatvaraju kut od \(45^\circ\).
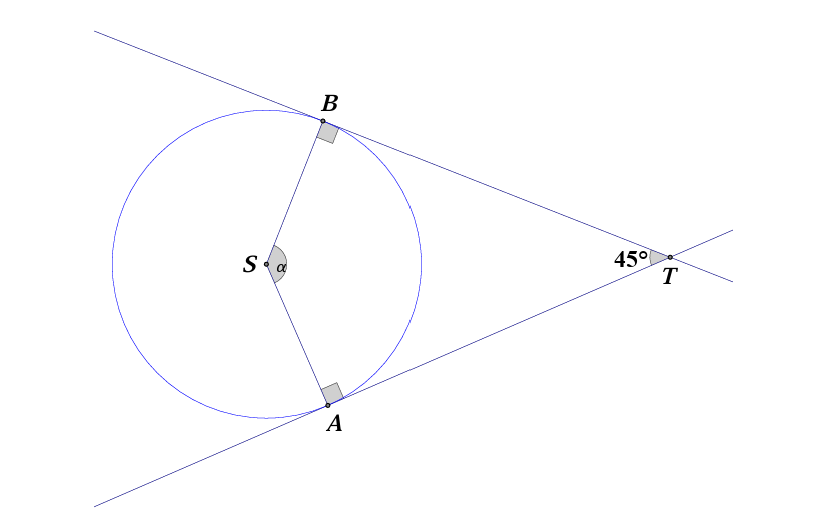
\textbf{Rješenje:}
\begin{center}
\includegraphics{tangente1.png}
\end{center}
Tangente su okomite na polumjere $\overline{AS}$ i $\overline{BS}$. Ta je činjenica jedna od najvjerojatnijih stvari koja će vam trebati čim se u zadatku spominju tangente pa uvijek prvo pokušajte vidjeti postoji li neka korisna dužina za koju bi se moglo primijeniti to pravilo, a da bi mogla ujedno još nečemu koristiti u zadatku.
Kutovi \(\angle ASB\) i \(\angle ATB\) su kutovi s okomitim kracima, od kojih je jedan šiljasti, a drugi tupi, pa vrijedi:
\[
\alpha = 180^\circ - 45^\circ = 135^\circ
\]
Duljinu kružnog luka računamo po formuli:
\[
l = \frac{\alpha}{180^\circ} \cdot \pi \cdot r
\]
Uvrštavanjem vrijednosti:
\[
l = \frac{135^\circ}{180^\circ} \cdot \pi \cdot 4 = 3 \pi
\]
Duljina kružnog luka koji se vidi iz točke \(T\) je:
\[
l = 3 \pi \ \text{cm}
\]
Kako se već koristi formula za duljinu kružnog luka, nevezano uz zadatak, ali korisno u tipovima zadataka gdje se traže nekakvi udjeli ili omjeri površina, površina kružnog isječka radijusa r i kuta alfa omeđenog u zadatku spomenutim kružnim lukom, dana je sličnom formulom kao i duljina luka:
\[
P = \frac{\alpha}{360^\circ} \cdot \pi \cdot r^2
\]
Kao rješenje ovog zadatka upišite, zaokružen na jednu decimalu, iznos površine koji bi imao kružni isječak omeđen kružnim lukom iz zadatka - dakle, radijusa kružnice 4 cm i kuta 135 stupnjeva.
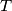 povučene su tangente na kružnicu polumjera
povučene su tangente na kružnicu polumjera 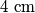 .
.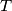 , ako tangente zatvaraju kut od
, ako tangente zatvaraju kut od 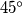 .
.
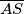 i
i 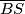 . Ta je činjenica jedna od najvjerojatnijih stvari koja će vam trebati čim se u zadatku spominju tangente pa uvijek prvo pokušajte vidjeti postoji li neka korisna dužina za koju bi se moglo primijeniti to pravilo, a da bi mogla ujedno još nečemu koristiti u zadatku.
. Ta je činjenica jedna od najvjerojatnijih stvari koja će vam trebati čim se u zadatku spominju tangente pa uvijek prvo pokušajte vidjeti postoji li neka korisna dužina za koju bi se moglo primijeniti to pravilo, a da bi mogla ujedno još nečemu koristiti u zadatku.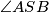 i
i 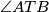 su kutovi s okomitim kracima, od kojih je jedan šiljasti, a drugi tupi, pa vrijedi:
su kutovi s okomitim kracima, od kojih je jedan šiljasti, a drugi tupi, pa vrijedi: 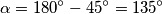
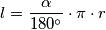 Uvrštavanjem vrijednosti:
Uvrštavanjem vrijednosti: 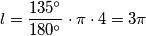
 je:
je: