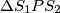Kružnice u ravnini - primjer 3
Sada kada smo upoznati s pojmovima vezanima uz položaj kružnica u ravnini, pogledajmo svojstva tangenti u slučaju dviju takvih kružnica na primjeru zadatka sa Školskog natjecanja za osme razrede iz 2019.
Zadatak:
Kružnice 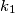 i
i 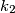 se dodiruju izvana. Omjer njihovih polumjera je 2:1. Zajednička tangenta dira kružnicu
se dodiruju izvana. Omjer njihovih polumjera je 2:1. Zajednička tangenta dira kružnicu 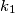 u točki T, a kružnicu
u točki T, a kružnicu 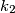 u točki
u točki  . Koliki je omjer duljine dužine
. Koliki je omjer duljine dužine 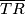 i polumjera veće kružnice?
i polumjera veće kružnice?
Rješenje:
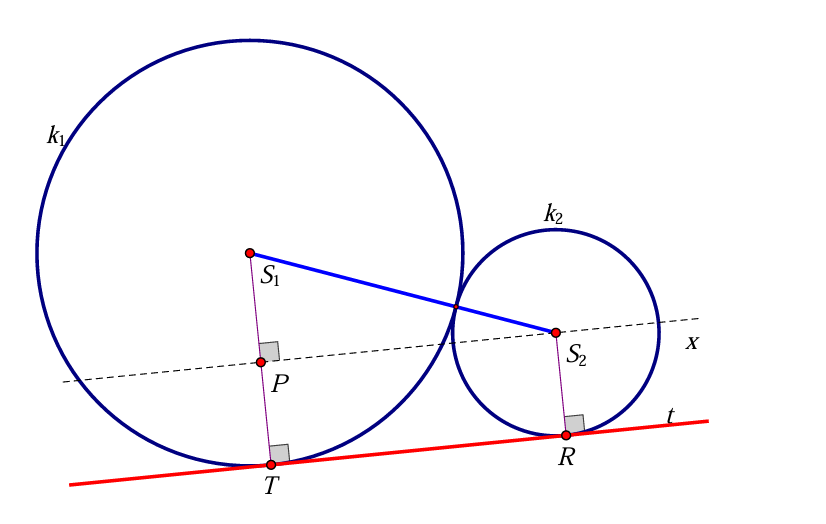
Označimo sa 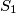 i
i 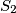 središta kružnica
središta kružnica 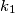 i
i 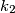 redom, kao i njihove polumjere
redom, kao i njihove polumjere 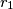 i
i 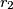 . Neka je
. Neka je 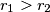 . Točkom
. Točkom 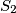 nacrtamo paralelu
nacrtamo paralelu  s
s 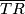 . Neka je
. Neka je 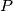 sjecište pravca
sjecište pravca  i polumjera kružnice
i polumjera kružnice 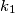 iz
iz 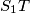 . Tada je
. Tada je 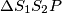 pravokutan, četverokut
pravokutan, četverokut 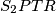 pravokutnik, pri čemu je
pravokutnik, pri čemu je 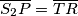 .
.
Primjenom Pitagorinog poučka dobivamo:
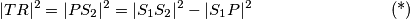
Iskoristimo omjer 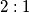 između polumjera kružnica
između polumjera kružnica 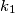 i
i 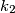 , kao i pretpostavku da je
, kao i pretpostavku da je 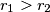 . Postoji broj
. Postoji broj  tako da možemo pisati:
tako da možemo pisati: 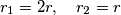
Tada je 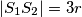
Uvrštavanjem u 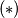 dobivamo:
dobivamo: 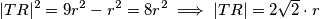
Pa je traženi omjer: 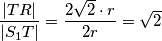
Ovdje smo ponovno koristili ključno svojstvo tangencijalnosti - radijus s tangentom u točki dirališta zatvara pravi kut i to vrijedi u svakoj kružnici za koju je dani pravac tangenta - u ovom slučaju, stoga, za obje.
Kao rješenje ovog zadatka upišite koliki je zbroj preostala dva kuta trokuta