Vrijeme: 10:10

Borba s nepoznatim #2

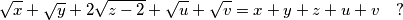
Koliko različitih uređenih petorki realnih brojeva (x,y,z,u,v) zadovoljava jednadžbu \begin{equation}\nonumber \sqrt{x}+\sqrt{y}+2\sqrt{z-2}+\sqrt{u}+\sqrt{v}=x+y+z+u+v \quad ? \end{equation}