Za  definiramo sljedeći sustav diofantskih jednadžbi:
definiramo sljedeći sustav diofantskih jednadžbi: 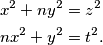
a) Pokaži da za beskonačno mnogo  sustav ima beskonačno mnogo prirodnih rješenja.
sustav ima beskonačno mnogo prirodnih rješenja.
b) Pokaži da za beskonačno mnogo  sustav nema prirodnih rješenja.
sustav nema prirodnih rješenja.
Za $n \in \mathbb{N}$ definiramo sljedeći sustav diofantskih jednadžbi:
\begin{align*}
x^2+ny^2&=z^2\\
nx^2+y^2&=t^2.
\end{align*}
a) Pokaži da za beskonačno mnogo $n$ sustav ima beskonačno mnogo prirodnih rješenja.
b) Pokaži da za beskonačno mnogo $n$ sustav nema prirodnih rješenja.