Vrijeme: 01:51
4.4.
Neka je dan tetivan četverokut  s opisanom kružnicom
s opisanom kružnicom  . Točke
. Točke  i
i  nalaze se na stranicama
nalaze se na stranicama  i
i  , redom, takve da je pravac
, redom, takve da je pravac  paralelan s pravcem
paralelan s pravcem  . Polupravci
. Polupravci 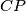 i
i 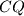 sijeku kružnicu
sijeku kružnicu  u točkama
u točkama  i
i  , redom. Neka je
, redom. Neka je 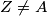 presjek kružnica opisanih trokutima
presjek kružnica opisanih trokutima 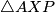 te
te 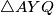 . Dokažite da se središte kružnice
. Dokažite da se središte kružnice  nalazi na pravcu
nalazi na pravcu 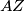 ako i samo ako je
ako i samo ako je  okomito na
okomito na  .
.
