Za pozitivne realne brojeve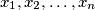 
vrijede sljedeće dvije nejednakosti: 
Koja je najmanji mogući 
?
Za pozitivne realne brojeve $x_1, x_2, \ldots, x_n$ vrijede sljedeće dvije nejednakosti:
$$ x_{1}^2 + x_{2}^2 + \ldots + x_{n}^2 < \frac{x_1 + x_2 + \ldots + x_n}{2};$$
$$ x_1 + x_2 + \ldots + x_n < \frac{x_{1}^3 + x_{2}^3 + \ldots + x_{n}^3}{2}. $$
Koja je najmanji mogući $n$?
