Uvedimo sada nove objekte koje ćemo zvati lanci. Svaki prirodan broj je lanac duljine \(1\) te svaki lanac duljine \(n \in \mathbb{N}\) nakon kojeg slijedi strelica \(\to\) i prirodan broj, skupa formiraju lanac duljine \(n+1\) (primjerice \(12 \to 3 \to 4 \to 3 \to 6\) je lanac duljine \(5\)). Svaki lanac reprezentira neki prirodan broj te kažemo da su dva lanca ekvivalentna ako reprezentiraju isti broj. Vrijede sljedeća pravila:\\
Neka su \(p,q,r\) prirodni brojevi i neka je \(X\) podlanac. Tada imamo:
\begin{enumerate}
\item Prazan lanac (ili lanac duljine \(0\)) reprezentira broj \(1\), a lanac \(p\) reprezentira broj \(p\).
\item \(X \to 1\) je ekvivalentno s \(X\).
\item \(p \to q \to r\) je ekvivalentno s \(p \uparrow ^r q\).
\item \(X \to 1 \to p\) je ekvivalentno s \(X\).
\item \(X \to (p+1) \to (q+1)\) je ekvivalentno s \(X \to (X \to p \to (q+1)) \to q\).
\end{enumerate}
Primijetimo da zbog \(p \to q \overset{(2)}{=} p \to q \to 1 \overset{(3)}{=} p \uparrow q = p^q\) možemo definirati \(p \to q = p^q\).\\
Odredi prirodan broj \(n\) u jednadžbi \(4 \to 3 \to 2 \to 2 = 4 \uparrow ^n 3\).
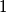 te svaki lanac duljine
te svaki lanac duljine 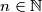 nakon kojeg slijedi strelica
nakon kojeg slijedi strelica  i prirodan broj, skupa formiraju lanac duljine
i prirodan broj, skupa formiraju lanac duljine 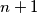 (primjerice
(primjerice 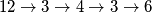 je lanac duljine
je lanac duljine 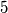 ). Svaki lanac reprezentira neki prirodan broj te kažemo da su dva lanca ekvivalentna ako reprezentiraju isti broj. Vrijede sljedeća pravila:
). Svaki lanac reprezentira neki prirodan broj te kažemo da su dva lanca ekvivalentna ako reprezentiraju isti broj. Vrijede sljedeća pravila: prirodni brojevi i neka je
prirodni brojevi i neka je  podlanac. Tada imamo:
podlanac. Tada imamo:  Primijetimo da zbog
Primijetimo da zbog 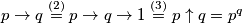 možemo definirati
možemo definirati  .
.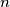 u jednadžbi
u jednadžbi  .
. 