Vrijeme: 22:05

Toto nismo više u Kansasu #2

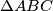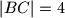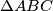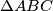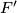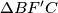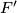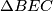Dan je fiksan šiljastokutan trokut \Delta ABC takav da je |BC|=4. Neka je točka F dana u trokutu \Delta ABC takva da zadovoljava svojstvo iz prošlog zadatka. Takvu točku ćemo nazvati izodinamičkom točkom \Delta ABC. Neka je F' izogonalna konjugata od F. Neka je E polovište luka kružnice opisane \Delta BF'C na kojemu se ne nalazi F'. Odredi površinu trokuta \Delta BEC.

Rješenje zaokruži na 3 decimale.