Marinada '20

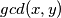Neka su $a,b,c$ cijeli brojevi različiti od nule, $n$ prirodan broj, a $p$ prost broj. $gcd(x,y)$ označava najveći zajednički djelitelj brojeva $x$ i $y$. U svakom zadatku pita se vrijedi li uvijek, odgovor je DA ako vrijedi za sve izbore brojeva, a NE ako postoji barem jedan slučaj u kojem ne vrijedi.\\ \begin{enumerate} \item Ako $a\mid bc$ i $gcd(b,c)=1$, mora li biti zadovoljena jedna od mogućnosti $a\mid b$ ili $a\mid c$? \item Ako $p\mid ab$, mora li biti zadovoljena jedna od mogućnosti $p\mid a$ ili $p\mid b$? \item Ako $ab\mid p$, mora li biti zadovoljena jedna od mogućnosti $a\mid p$ ili $b\mid p$? \item Ako $p\mid a+b$, mora li biti zadovoljena jedna od mogućnosti $p\mid a$ ili $p\mid b$? \item Ako $p\mid a^n$, mora li biti $p^n\mid a^n$? \end{enumerate}\\ Rješenje zapišite u obliku niza slova $D$ (za odgovor DA) i $N$ (za odgovor NE), bez zareza, pri čemu prvo slovo odgovara odgovoru na prvo pitanje, drugo slovo odgovoru na drugo pitanje itd.\\ Primjer: $DDDNN$