(Općinsko natjecanje 2007., 1. razred) Postoji li pravokutan trokut kojemu su duljine kateta cijeli brojevi, a duljina hipotenuze 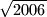 ?
?
Rješenje.
1. Razumijevanje problema.
,,Što je nepoznato?'' Postojanje pravokutnog trokuta.
,,Što su poznati podatci?'' Duljine kateta su cijeli brojevi, a hipotenuza je duljine 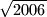 .
.
,,Prikladno označimo veličine.'' Ako taj trokut postoji, označimo mu duljine kateta sa  i
i  .
.
,,Što povezuje ove veličine?'' Kada bi taj pravokutan trokut postojao, na njega bi se mogao primijeniti Pitagorin poučak.
2. Smišljanje plana.
Kada treba odrediti postoji li nešto, važno je odabrati hoćemo li krenuti od pretpostavke da tražena stvar postoji ili ne. U ovom slučaju, ako bismo pretpostavili da trokut ne postoji, nemamo od čega krenuti, stoga pretostavimo da trokut postoji.
Sada možemo primijeniti Pitagorin poučak pa imamo 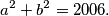 Ovo je jedna jednadžba, ali imamo dvije nepoznanice. Uvjet zadatka je da su
Ovo je jedna jednadžba, ali imamo dvije nepoznanice. Uvjet zadatka je da su  i
i  cijeli brojevi, stoga je ovdje riječ o
cijeli brojevi, stoga je ovdje riječ o 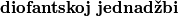 .
.
Naš početni problem može se preformulirati na sljedeći način: ,,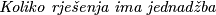
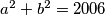 ?''
?''
Jesmo li iskoristili sve uvjete u zadatku? Još nismo koristili uvjet da su  i
i  cijeli brojevi. Kakvi mogu biti cijeli brojevi? Pozitivni i negativni (i nula), ali negativni brojevi (i nula) u ovom kontekstu nemaju ni smisla jer
cijeli brojevi. Kakvi mogu biti cijeli brojevi? Pozitivni i negativni (i nula), ali negativni brojevi (i nula) u ovom kontekstu nemaju ni smisla jer  i
i  predstavljaju duljine kateta.
predstavljaju duljine kateta.
Koje svojstvo imaju cijeli brojevi, a racionalni i realni brojevi nemaju? Parnost i neparnost, pa pogledajmo možemo li to nekako iskoristiti. Najprije uočimo kako je broj 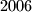 paran pa zbroj
paran pa zbroj 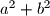 mora biti paran. Kada je zbroj paran? Kada su pribrojnici iste parnosti pa ćemo imati dva slučaja.
mora biti paran. Kada je zbroj paran? Kada su pribrojnici iste parnosti pa ćemo imati dva slučaja.
Brojevi  i
i 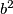 su kvadrati. Kada su kvadrati parni ili neparni? Ako nismo otprije upoznati s tim rezultatom, to također treba istražiti. Ispitujući na par primjera, možemo naslutiti da su kvadrati parnih brojeva parni, a kvadrati neparnih brojeva neparni. Vrijedi li i nešto više?
su kvadrati. Kada su kvadrati parni ili neparni? Ako nismo otprije upoznati s tim rezultatom, to također treba istražiti. Ispitujući na par primjera, možemo naslutiti da su kvadrati parnih brojeva parni, a kvadrati neparnih brojeva neparni. Vrijedi li i nešto više?
Kvadrat parnog broja je djeljiv s  , a kvadrat neparnog broja pri dijeljenju s
, a kvadrat neparnog broja pri dijeljenju s  daje ostatak
daje ostatak  (Možete li to dokazati?). Promislimo: ako su oba pribrojnika djeljiva s
(Možete li to dokazati?). Promislimo: ako su oba pribrojnika djeljiva s  , mora li zbroj biti djeljiv s
, mora li zbroj biti djeljiv s  ? Koliki je zbroj?
? Koliki je zbroj?
Dakle, rješenje zadatka ovisi o pitanju može li zbroj dva neparna kvadrata biti 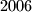 , a to možemo algebarski ispitati.
, a to možemo algebarski ispitati.
Imamo plan!
3. Provođenje plana.
Pretpostavimo da takav pravokutan trokut postoji, stoga vrijedi 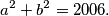 Budući da je
Budući da je 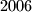 paran broj, to također mora biti zbroj na lijevoj strani jednadžbe pa su
paran broj, to također mora biti zbroj na lijevoj strani jednadžbe pa su  i
i 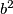 ili oba parna ili oba neparna. Slučaj kada su oba ta pribrojnika parna otpada jer su tada djeljivi s
ili oba parna ili oba neparna. Slučaj kada su oba ta pribrojnika parna otpada jer su tada djeljivi s  pa i njihov zbroj mora biti djeljiv s
pa i njihov zbroj mora biti djeljiv s  , a
, a 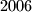 nije djeljiv s
nije djeljiv s  pa taj slučaj otpada.
pa taj slučaj otpada.
Dakle,  i
i 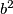 su neparni brojevi, što znači da su
su neparni brojevi, što znači da su  i
i  neparni. Tada možemo zapisati
neparni. Tada možemo zapisati 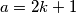 ,
, 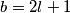 , gdje su
, gdje su  i
i  cijeli brojevi.
cijeli brojevi.
Slijedi: 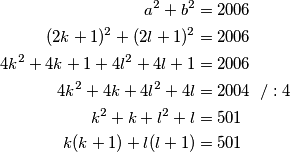 Brojevi
Brojevi  i
i  su različitih parnosti pa je njihov umnožak paran broj, stoga je zbroj na lijevoj strani paran, a broj
su različitih parnosti pa je njihov umnožak paran broj, stoga je zbroj na lijevoj strani paran, a broj 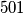 neparan. Krenuli smo od pretpostavke da pravokutan trokut sa zadanim uvjetom postoji i došli smo do nečeg nemogućeg pa je zaključak da je početna pretpostavka bila netočna, odnosno traženi trokut ne postoji.
neparan. Krenuli smo od pretpostavke da pravokutan trokut sa zadanim uvjetom postoji i došli smo do nečeg nemogućeg pa je zaključak da je početna pretpostavka bila netočna, odnosno traženi trokut ne postoji.
4. Osvrt Kada radimo osvrt na ovakav zadatak, dobro se uvjeriti da je svaki korak u rješavanju valjan. Primjerice, je li svaki kvadrat parnog broja djeljv s  ? Provjerimo:
? Provjerimo: 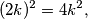 čime je tvrdnja vrlo lako dokazana.
čime je tvrdnja vrlo lako dokazana.
Također, svaki kvadrat neparnog brojeva pri djeljenju s 4 daje ostatak  zato što:
zato što:  U zadnjem koraku smo koristili činjenicu da je umnožak parnog i neparnog broja paran. Pokušajte to dokazati sami.
U zadnjem koraku smo koristili činjenicu da je umnožak parnog i neparnog broja paran. Pokušajte to dokazati sami.
Kao rješenje upišite 0.
\textit{(Općinsko natjecanje 2007., 1. razred)} Postoji li pravokutan trokut kojemu su duljine kateta cijeli brojevi, a duljina hipotenuze $\sqrt{2006}$?
\\\\
\emph{Rješenje.} \\\\
\textbf{1. Razumijevanje problema.} \\\\
,,\textit{Što je nepoznato?}'' Postojanje pravokutnog trokuta. \\\\
,,\textit{Što su poznati podatci?}'' Duljine kateta su cijeli brojevi, a hipotenuza je duljine $\sqrt{2006}$. \\\\
,,\textit{Prikladno označimo veličine.}'' Ako taj trokut postoji, označimo mu duljine kateta sa $a$ i $b$. \\\\
,,\textit{Što povezuje ove veličine?}'' Kada bi taj pravokutan trokut postojao, na njega bi se mogao primijeniti Pitagorin poučak. \\\\
\textbf{2. Smišljanje plana.} \\\\
Kada treba odrediti postoji li nešto, važno je odabrati hoćemo li krenuti od pretpostavke da tražena stvar postoji ili ne. U ovom slučaju, ako bismo pretpostavili da trokut ne postoji, nemamo od čega krenuti, stoga pretostavimo da trokut postoji.
\\\\
Sada možemo primijeniti Pitagorin poučak pa imamo
$$
a^2+b^2=2006.
$$
Ovo je jedna jednadžba, ali imamo dvije nepoznanice. Uvjet zadatka je da su $a$ i $b$ cijeli brojevi, stoga je ovdje riječ o $\textbf{diofantskoj jednadžbi}$.
\\\\
Naš početni problem može se preformulirati na sljedeći način: ,,$\textit{Koliko rješenja ima jednadžba}$ $a^2+b^2=2006$?'' \\\\
Jesmo li iskoristili sve uvjete u zadatku? Još nismo koristili uvjet da su $a$ i $b$ cijeli brojevi. Kakvi mogu biti cijeli brojevi? Pozitivni i negativni (i nula), ali negativni brojevi (i nula) u ovom kontekstu nemaju ni smisla jer $a$ i $b$ predstavljaju duljine kateta. \\\\
Koje svojstvo imaju cijeli brojevi, a racionalni i realni brojevi nemaju? Parnost i neparnost, pa pogledajmo možemo li to nekako iskoristiti. Najprije uočimo kako je broj $2006$ paran pa zbroj $a^2+b^2$ mora biti paran. Kada je zbroj paran? Kada su pribrojnici iste parnosti pa ćemo imati dva slučaja.
\\\\
Brojevi $a^2$ i $b^2$ su kvadrati. Kada su kvadrati parni ili neparni? Ako nismo otprije upoznati s tim rezultatom, to također treba istražiti. Ispitujući na par primjera, možemo naslutiti da su kvadrati parnih brojeva parni, a kvadrati neparnih brojeva neparni. Vrijedi li i nešto više?
\\\\
Kvadrat parnog broja je djeljiv s $4$, a kvadrat neparnog broja pri dijeljenju s $4$ daje ostatak $1$ (\textit{Možete li to dokazati?}). Promislimo: ako su oba pribrojnika djeljiva s $4$, mora li zbroj biti djeljiv s $4$? Koliki je zbroj?
\\\\
Dakle, rješenje zadatka ovisi o pitanju može li zbroj dva neparna kvadrata biti $2006$, a to možemo algebarski ispitati. \\\\
Imamo plan! \\\\
\textbf{3. Provođenje plana.} \\\\
Pretpostavimo da takav pravokutan trokut postoji, stoga vrijedi
$$
a^2+b^2=2006.
$$
Budući da je $2006$ paran broj, to također mora biti zbroj na lijevoj strani jednadžbe pa su $a^2$ i $b^2$ ili oba parna ili oba neparna. Slučaj kada su oba ta pribrojnika parna otpada jer su tada djeljivi s $4$ pa i njihov zbroj mora biti djeljiv s $4$, a $2006$ nije djeljiv s $4$ pa taj slučaj otpada. \\\\
Dakle, $a^2$ i $b^2$ su neparni brojevi, što znači da su $a$ i $b$ neparni. Tada možemo zapisati $a=2k+1$, $b=2l+1$, gdje su $k$ i $l$ cijeli brojevi.
\\\\
Slijedi:
\begin{align*}
a^2+b^2&=2006 \\
(2k+1)^2+(2l+1)^2&=2006 \\
4k^2+4k+1+4l^2+4l+1&=2006 \\
4k^2+4k+4l^2+4l&=2004 \hspace{0.2cm}/ : 4 \\
k^2+k+l^2+l&=501 \\
k(k+1)+l(l+1)&=501
\end{align*}
Brojevi $k$ i $k+1$ su različitih parnosti pa je njihov umnožak paran broj, stoga je zbroj na lijevoj strani paran, a broj $501$ neparan. Krenuli smo od pretpostavke da pravokutan trokut sa zadanim uvjetom postoji i došli smo do nečeg nemogućeg pa je zaključak da je početna pretpostavka bila netočna, odnosno traženi trokut ne postoji.
\\\\
\textbf{4. Osvrt} Kada radimo osvrt na ovakav zadatak, dobro se uvjeriti da je svaki korak u rješavanju valjan. Primjerice, je li svaki kvadrat parnog broja djeljv s $4$? Provjerimo:
$$
(2k)^2=4k^2,
$$
čime je tvrdnja vrlo lako dokazana.
\\\\
Također, svaki kvadrat neparnog brojeva pri djeljenju s 4 daje ostatak $1$ zato što:
$$
(2k+1)^2=4k^2+4k+1=4(\underbrace{k^2+k}_{\in \mathbb{Z}})+1.
$$
U zadnjem koraku smo koristili činjenicu da je umnožak parnog i neparnog broja paran. Pokušajte to dokazati sami.
Kao rješenje upišite 0.
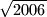 ?
? 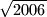 .
.  i
i  .
. 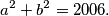 Ovo je jedna jednadžba, ali imamo dvije nepoznanice. Uvjet zadatka je da su
Ovo je jedna jednadžba, ali imamo dvije nepoznanice. Uvjet zadatka je da su  i
i  cijeli brojevi, stoga je ovdje riječ o
cijeli brojevi, stoga je ovdje riječ o 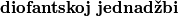 .
. 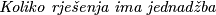
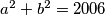 ?''
?''  i
i  cijeli brojevi. Kakvi mogu biti cijeli brojevi? Pozitivni i negativni (i nula), ali negativni brojevi (i nula) u ovom kontekstu nemaju ni smisla jer
cijeli brojevi. Kakvi mogu biti cijeli brojevi? Pozitivni i negativni (i nula), ali negativni brojevi (i nula) u ovom kontekstu nemaju ni smisla jer  i
i  predstavljaju duljine kateta.
predstavljaju duljine kateta. 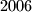 paran pa zbroj
paran pa zbroj 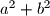 mora biti paran. Kada je zbroj paran? Kada su pribrojnici iste parnosti pa ćemo imati dva slučaja.
mora biti paran. Kada je zbroj paran? Kada su pribrojnici iste parnosti pa ćemo imati dva slučaja.  i
i 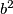 su kvadrati. Kada su kvadrati parni ili neparni? Ako nismo otprije upoznati s tim rezultatom, to također treba istražiti. Ispitujući na par primjera, možemo naslutiti da su kvadrati parnih brojeva parni, a kvadrati neparnih brojeva neparni. Vrijedi li i nešto više?
su kvadrati. Kada su kvadrati parni ili neparni? Ako nismo otprije upoznati s tim rezultatom, to također treba istražiti. Ispitujući na par primjera, možemo naslutiti da su kvadrati parnih brojeva parni, a kvadrati neparnih brojeva neparni. Vrijedi li i nešto više?  , a kvadrat neparnog broja pri dijeljenju s
, a kvadrat neparnog broja pri dijeljenju s  daje ostatak
daje ostatak  (Možete li to dokazati?). Promislimo: ako su oba pribrojnika djeljiva s
(Možete li to dokazati?). Promislimo: ako su oba pribrojnika djeljiva s  , mora li zbroj biti djeljiv s
, mora li zbroj biti djeljiv s  ? Koliki je zbroj?
? Koliki je zbroj? 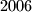 , a to možemo algebarski ispitati.
, a to možemo algebarski ispitati. 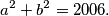 Budući da je
Budući da je 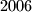 paran broj, to također mora biti zbroj na lijevoj strani jednadžbe pa su
paran broj, to također mora biti zbroj na lijevoj strani jednadžbe pa su  i
i 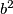 ili oba parna ili oba neparna. Slučaj kada su oba ta pribrojnika parna otpada jer su tada djeljivi s
ili oba parna ili oba neparna. Slučaj kada su oba ta pribrojnika parna otpada jer su tada djeljivi s  pa i njihov zbroj mora biti djeljiv s
pa i njihov zbroj mora biti djeljiv s  , a
, a 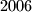 nije djeljiv s
nije djeljiv s  pa taj slučaj otpada.
pa taj slučaj otpada.  i
i 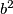 su neparni brojevi, što znači da su
su neparni brojevi, što znači da su  i
i  neparni. Tada možemo zapisati
neparni. Tada možemo zapisati 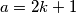 ,
, 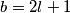 , gdje su
, gdje su  i
i  cijeli brojevi.
cijeli brojevi. 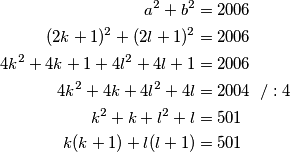 Brojevi
Brojevi  i
i  su različitih parnosti pa je njihov umnožak paran broj, stoga je zbroj na lijevoj strani paran, a broj
su različitih parnosti pa je njihov umnožak paran broj, stoga je zbroj na lijevoj strani paran, a broj 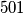 neparan. Krenuli smo od pretpostavke da pravokutan trokut sa zadanim uvjetom postoji i došli smo do nečeg nemogućeg pa je zaključak da je početna pretpostavka bila netočna, odnosno traženi trokut ne postoji.
neparan. Krenuli smo od pretpostavke da pravokutan trokut sa zadanim uvjetom postoji i došli smo do nečeg nemogućeg pa je zaključak da je početna pretpostavka bila netočna, odnosno traženi trokut ne postoji.  ? Provjerimo:
? Provjerimo: 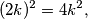 čime je tvrdnja vrlo lako dokazana.
čime je tvrdnja vrlo lako dokazana.  zato što:
zato što:  U zadnjem koraku smo koristili činjenicu da je umnožak parnog i neparnog broja paran. Pokušajte to dokazati sami.
U zadnjem koraku smo koristili činjenicu da je umnožak parnog i neparnog broja paran. Pokušajte to dokazati sami.