Zadataci iz ovoga lanca preuzeti su iz uvoda knjige ,,Problem Solving Through Problems'' autora Lorena C. Larsona.
Preporučamo da svoj proces rješavanja uskladite s Polyinim koracima, ili barem da naknadno pokušate prepoznati njegove  faze rješavanja matematičkog problema.
faze rješavanja matematičkog problema.
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Neka je 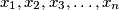 niz realnih brojeva različitih od nule za koji vrijedi:
niz realnih brojeva različitih od nule za koji vrijedi: 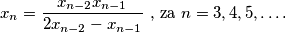
Odredite nužne i dovoljne uvjete na  i
i 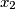 tako da je
tako da je 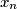 cijeli broj za beskonačno mnogo vrijednosti od
cijeli broj za beskonačno mnogo vrijednosti od  .
.
Zadataci iz ovoga lanca preuzeti su iz uvoda knjige ,,Problem Solving Through Problems'' autora Lorena C. Larsona.
Preporučamo da svoj proces rješavanja uskladite s Polyinim koracima, ili barem da naknadno pokušate prepoznati njegove $4$ faze rješavanja matematičkog problema.
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Neka je $x_1, x_2, x_3, \dots, x_n$ niz realnih brojeva različitih od nule za koji vrijedi:
\[ x_n = \dfrac{x_{n-2} x_{n-1}}{2x_{n-2} - x_{n-1}} \text{ , za } n=3, 4, 5, \dots \text{.} \]
Odredite nužne i dovoljne uvjete na $x_1$ i $x_2$ tako da je $x_n$ cijeli broj za beskonačno mnogo vrijednosti od $n$.
 faze rješavanja matematičkog problema.
faze rješavanja matematičkog problema.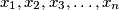 niz realnih brojeva različitih od nule za koji vrijedi:
niz realnih brojeva različitih od nule za koji vrijedi: 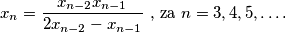
 i
i 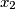 tako da je
tako da je 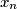 cijeli broj za beskonačno mnogo vrijednosti od
cijeli broj za beskonačno mnogo vrijednosti od  .
. 