MetaMath '22

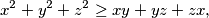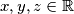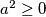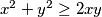\textbf{Primjer 1:} Dokažite nejednakost: \begin{equation*} x^2 + y^2 + z^2 \geq xy + yz + zx\text, \end{equation*} za sve $x,y,z \in \mathbb R$. \textbf{Rješenje:} Jedno od rješenja je svođenje na osnovnu nejednakost realnih brojeva: $a^2\geq0$ za sve realne brojeve $a$. Dokažimo da vrijedi $x^2 + y^2 \geq 2xy$. Imamo redom niz ekvivalentnih nejednakosti: 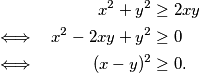\begin{alignat*}{2} & &x^2 + y^2 &\geq 2xy \\ &\iff \quad&x^2-2xy+y^2 &\geq 0 \\ &\iff \quad &(x-y)^2 &\geq 0 \text. \end{alignat*} Kako je posljednja nejednakost istinita, zaključujemo da vrijedi i 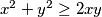$x^2 + y^2 \geq 2xy$. Analogno dobivamo: 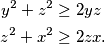\begin{align*} y^2 + z^2 &\geq 2yz \\ z^2 + x^2 &\geq 2zx\text. \end{align*} Zbrojimo li tri dobivene nejednakosti dobivamo: 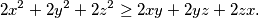\begin{equation*} 2x^2+2y^2+2z^2 \geq 2xy+2yz+2zx\text. \end{equation*} Dijeljenjem s $2$ dobijemo točno traženu nejednakost. Drugo rješenje može biti iskoristi 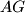$AG$ nejednakost. Kako je 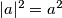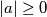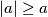$|a|^2=a^2$, $|a|\geq0$, $|a|\geq a$ za sve realne brojeve $a$, vrijedi: \begin{equation*} \frac{x^2+y^2}{2}=\frac{|x|^2+|y|^2}{2}\overset{AG}{\geq}\sqrt{|x|^2\cdot|y|^2}=|xy|\geq xy\text. 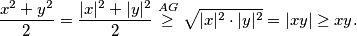\end{equation*} Sasvim identično dobivamo nejednakosti: 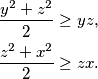\begin{align*} \frac{y^2+z^2}{2} &\geq yz\text, \\ \frac{z^2+x^2}{2} &\geq zx\text. \end{align*} Zbrajanjem triju nejednakosti dobijemo 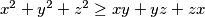$x^2+y^2+z^2\geq xy+yz+zx$ što je i trebalo dokazati. \textit{Kako biste dobili 1 bod za ovaj primjer unesite 1 kao rješenje.}