\textbf{Primjer 2:}
Ako su $a$, $b$, $c$ duljine stranica trokuta, dokažite da je:
\begin{equation*}
\frac{a}{b+c-a} + \frac{b}{c+a-b} + \frac{c}{a+b-c} \geq 3\text.
\end{equation*}
\textbf{Rješenje:}
Poznato je da u trokutu vrijedi nejednakost: zbroj duljina dviju stranica je strogo veća od duljine treće stranice, što se naziva i \textit{nejednakost trokuta}. Stoga su svi nazivnici u traženoj nejednakosti dobro definirani (različiti od nule) i pozitivni. Uvedimo \textbf{supstituciju}:
\begin{align*}
x &= b+c-a \\
y &= c+a-b \\
z &= a+b-c \text,
\end{align*}
iz čega dobivamo \begin{equation*}
a=\frac{y+z}{2}, \quad b=\frac{z+x}{2}, \quad c=\frac{x+y}{2}\text.
\end{equation*}
Označimo s $LHS$ lijevu stranu početne tražene nejednakosti. Vrijedi:
\begin{align*}
LHS = \frac{y+z}{2x} + \frac{z+x}{2y} + \frac{x+y}{2z}\text.
\end{align*}
Postoji više načina kako dokazati da je dobiveni izraz veći ili jednak od $3$.
\textit{Prvi način}:
\begin{align*}
LHS &= \frac{y+z}{2x} + \frac{z+x}{2y} + \frac{x+y}{2z} \\
&= \frac{1}{2}\left( \frac{x}{y} + \frac{y}{x} + \frac{y}{z} + \frac{z}{y} + \frac{z}{x} + \frac{x}{z} \right) \\
&\overset{AG}{\geq} \frac{1}{2} \left(2\cdot \sqrt{\frac{x}{y}\cdot \frac{y}{x}} + 2\cdot \sqrt{\frac{y}{z}\cdot \frac{z}{y}} + 2\cdot \sqrt{\frac{z}{x}\cdot \frac{x}{z}}\right) \\
&= 3\text.
\end{align*}
\textit{Drugi način}:
\begin{align*}
2LHS&= \frac{y+z}{x} +\frac{z+x}{y}+\frac{x+y}{z} \\
2LHS +3&= \frac{y+z}{x} + 1 + \frac{z+x}{y}+ 1 + \frac{x+y}{z}+ 1 \\
&= (x+y+z)\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)\text.
\end{align*}
Primijetimo što dobivamo iz aritmetičko harmonijske sredine:
\begin{equation*}
\frac{x+y+z}{3} \overset{AH}{\geq} \frac{3}{\frac{1}{x} + \frac{1}{y} + \frac{1}{z}}
\end{equation*}
iz čega slijedi
\begin{equation*}
(x+y+z)\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right) \geq 9\text.
\end{equation*}
Ova nejednakost može se dobiti i iz $CSB$ nejednakosti:
\begin{equation*}
(x+y+z)\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right) \overset{CSB}{\geq} \left( \sqrt{x\cdot \frac{1}{x}} + \sqrt{y\cdot \frac{1}{y}} + \sqrt{z\cdot \frac{1}{z}} \right)^2=9
\end{equation*}
Konačno, imamo:
\begin{align*}
2LHS + 3&= (x+y+z)\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right) \geq 9\text.
\end{align*}
Iz posljednjeg zaključujemo $LHS\geq 3$ čime je tražena nejednakost dokazana.
\textit{Kako biste dobili 1 bod za ovaj primjer unesite 2 kao rješenje.}
, 
, 
duljine stranica trokuta, dokažite da je: 
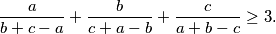
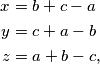iz čega dobivamo 
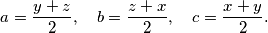Označimo s 
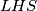lijevu stranu početne tražene nejednakosti. Vrijedi: 
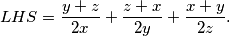Postoji više načina kako dokazati da je dobiveni izraz veći ili jednak od 
.
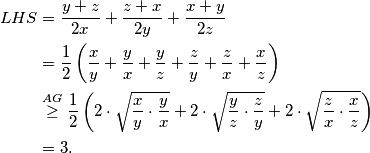
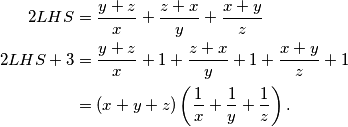Primijetimo što dobivamo iz aritmetičko harmonijske sredine: 
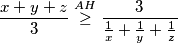iz čega slijedi 
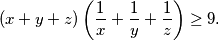Ova nejednakost može se dobiti i iz 
nejednakosti: 
Konačno, imamo: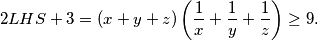 
Iz posljednjeg zaključujemo 
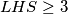čime je tražena nejednakost dokazana.