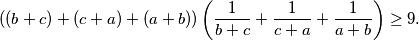\textbf{Primjer 3:} [\textit{Nesbittova nejednakost}]
Dokažite da za sve pozitivne realne brojeve $a$, $b$, $c$ vrijedi nejednakost:
\begin{equation*}
\frac{a}{b+c} + \frac{b}{c+a} +\frac{c}{a+b} \geq \frac{3}{2}\text.
\end{equation*}
\textbf{Rješenje:}
Primjenom \textit{CSB} nejednakosti dobivamo:
\begin{equation*}
\left(\frac{a}{b+c} + \frac{b}{c+a} +\frac{c}{a+b}\right) \cdot \left(a(b+c)+b(c+a)+c(a+b)\right) \overset{CSB}{\geq} (a+b+c)^2\text.
\end{equation*}
Označimo s \textit{LHS} lijevi izraz u traženoj nejednakosti, tj.
\begin{equation*}
LHS = \frac{a}{b+c} + \frac{b}{c+a} +\frac{c}{a+b}\text.
\end{equation*}
Iz dobivene nejednakosti zaključujemo:
\begin{equation*}
LHS \cdot 2(ab+bc+ca) \geq (a+b+c)^2\text.
\end{equation*}
Nadalje, imamo:
\begin{align*}
LHS &\geq \frac{(a+b+c)^2}{2(ab+bc+ca)} \\
&= \frac{a^2+b^2+c^2 + 2ab+2bc+2ca}{2(ab+bc+ca)}\\
&\geq \frac{ab+bc+ca + 2ab+2bc+2ca}{2(ab+bc+ca)}\\
&=\frac{3(ab+bc+ca)}{2(ab+bc+ca)}\\
&=\frac{3}{2}\text.
\end{align*}
Posljednja nejednakost vrijedi iz već dokazane nejednakosti iz Primjera 1, $a^2+b^2+c^2\geq ab+bc+ca$. S time smo dobili $LHS\geq\frac{3}{2}$ što je i trebalo dokazati.
\textit{Drugi dokaz}.
Neka je \textit{LHS} isti izraz kao u prvom rješenju (lijeva strana tražene nejednakosti). Promotrimo izraz:
\begin{align*}
LHS+3 &= \frac{a}{b+c}+1+\frac{b}{c+a}+1+\frac{c}{a+b}+1\\
&= \frac{a+b+c}{b+c}+\frac{a+b+c}{c+a}+\frac{a+b+c}{a+b}\\
&=(a+b+c)\left(\frac{1}{b+c}+\frac{1}{c+a}+\frac{1}{a+b}\right)\\
&= \frac{1}{2}\cdot ((b+c)+(c+a)+(a+b))\left(\frac{1}{b+c}+\frac{1}{c+a}+\frac{1}{a+b}\right)\\
&\overset{CSB}{\geq} \frac{1}{2}\cdot \left(\sqrt{\frac{b+c}{b+c}} + \sqrt{\frac{c+a}{c+a}} + \sqrt{\frac{a+b}{a+b}}\right)^2\\
&=\frac{9}{2}\text.
\end{align*}
Dobili smo $LHS+3\geq\frac{9}{2}$, iz čega slijedi $LHS\geq\frac{3}{2}$.
Umjesto \textit{CSB} nejednakosti u zadnjem koraku mogli smo koristiti i \textit{AH} nejednakost. Kako su $a,b,c>0$ vrijedi:
\begin{equation*}
\frac{(b+c)+(c+a)+(a+b)}{3} \overset{AH}{\geq} \frac{3}{\frac{1}{b+c}+\frac{1}{c+a}+\frac{1}{a+b}}\text,
\end{equation*}
iz čega zaključujemo
\begin{equation*}
((b+c)+(c+a)+(a+b))\left(\frac{1}{b+c}+\frac{1}{c+a}+\frac{1}{a+b}\right) \geq 9\text.
\end{equation*}
\textit{Za dobivanje 1 boda unesite 3 kao rješenje.}
, 
, 
vrijedi nejednakost: 
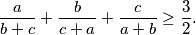
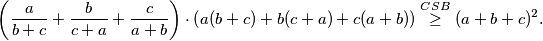Označimo s LHS lijevi izraz u traženoj nejednakosti, tj. 
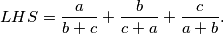Iz dobivene nejednakosti zaključujemo: 
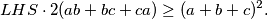Nadalje, imamo: 
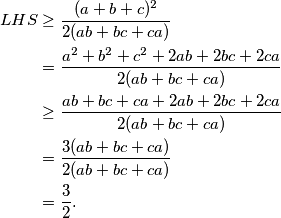Posljednja nejednakost vrijedi iz već dokazane nejednakosti iz Primjera 1, 
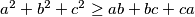. S time smo dobili 
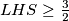što je i trebalo dokazati.
Dobili smo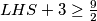 
, iz čega slijedi 
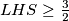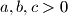vrijedi: 
iz čega zaključujemo 