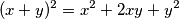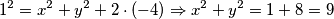Primjer 2. Neka su  i
i  realni brojevi takvi da vrijedi
realni brojevi takvi da vrijedi 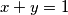 i
i 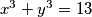 . Koliko je
. Koliko je 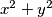 ?
?
RJEŠENJE.
Kako u zadatku imamo zadan zbroj kubova raspisati ćemo formulu za kub binoma zbroja kako bismo kasnije zadane jednakosti mogli uvrstiti u nju.
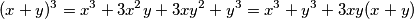
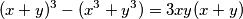
Sada možemo uvrstiti dane jednakosti iz zadatka. 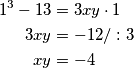
Sada zamijetimo kako nam se 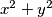 nalazi u formuli za kvadrat zbroja te imamo
nalazi u formuli za kvadrat zbroja te imamo
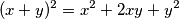
Uvrsimo ono što znamo i imamo;
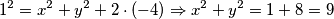
*Kako biste dobili 1 bod unesite 5 kao rješenje.
Primjer 2. Neka su $x$ i $y$ realni brojevi takvi da vrijedi $x + y = 1$ i $x^3 + y^3 = 13$. Koliko je $x^2 + y^2$?\\
RJEŠENJE.\\
Kako u zadatku imamo zadan zbroj kubova raspisati ćemo formulu za kub binoma zbroja kako bismo kasnije zadane jednakosti mogli uvrstiti u nju.\\
$$(x + y)^3 = x^3 + 3x^2y + 3xy^2 + y^3 = x^3 + y^3 + 3xy(x + y)$$
$$(x + y)^3 - (x^3 + y^3) = 3xy(x + y)$$
Sada možemo uvrstiti dane jednakosti iz zadatka.
\begin{align*}
1^3 - 13 &= 3xy \cdot 1\\
3xy &= - 12 /:3\\
xy &= - 4 \\
\end{align*}
Sada zamijetimo kako nam se $x^2 + y^2$ nalazi u formuli za kvadrat zbroja te imamo
$$(x + y)^2 = x^2 + 2xy + y^2$$
Uvrsimo ono što znamo i imamo;
$$1^2 = x^2 + y^2 + 2 \cdot (-4) \Rightarrow x^2 + y^2 = 1 + 8 = 9$$
\\
*Kako biste dobili 1 bod unesite 5 kao rješenje.
 i
i  realni brojevi takvi da vrijedi
realni brojevi takvi da vrijedi 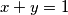 i
i 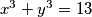 . Koliko je
. Koliko je 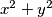 ?
?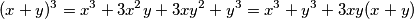
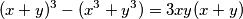
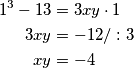
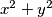 nalazi u formuli za kvadrat zbroja te imamo
nalazi u formuli za kvadrat zbroja te imamo