MetaMath '22

Primjer 3. Odredi najmanju moguću vrijednost izraza 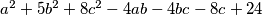$a^2 + 5b^2 + 8c^2 - 4ab - 4bc - 8c + 24$, pri čemu su $a$, $b$ i $c$ realni brojevi, te odredi $a$, $b$ i $c$ za koje se ta vrijednost postiže. RJEŠENJE.\\ Zadani izraz potrebno je zapisati na sljedeći način; 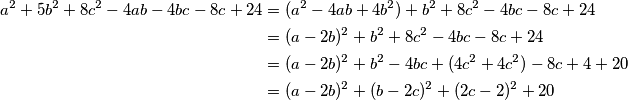\begin{align*} a^2 + 5b^2 + 8c^2 - 4ab - 4bc - 8c + 24 &= (a^2 - 4ab + 4b^2) + b^2 + 8c^2 - 4bc - 8c + 24\\ &=(a - 2b)^2 + b^2 + 8c^2 - 4bc - 8c + 24 \\ &=(a - 2b)^2 + b^2 - 4bc + (4c^2 + 4c^2) - 8c + 4 + 20\\ &=(a - 2b)^2 + (b - 2c)^2 + (2c - 2)^2 + 20\\ \end{align*} Vidljivo je kako je svaki od kvadriranih izraza veći ili jednak od 0 te slijedi;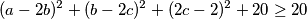 $$(a - 2b)^2 + (b - 2c)^2 + (2c - 2)^2 + 20 \geq 20$$ Zaključujemo kako je najmanja vrijednost koju izraz može postići 20, a to će biti onda kada su kvadrirani izrazi jednaki 0. 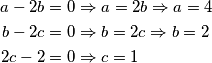\begin{align*} a - 2b &= 0 \Rightarrow a = 2b \Rightarrow a = 4\\ b - 2c &= 0 \Rightarrow b = 2c \Rightarrow b = 2\\ 2c - 2 &= 0 \Rightarrow c = 1 \\ \end{align*} \\ *Kako biste dobili 1 bod unesite 6 kao rješenje.