ZADATAK 4. Ako su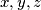 
i 
pozitivni realni brojevi takvi da vrijedi
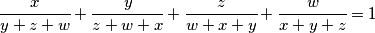
odredi
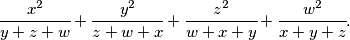
ZADATAK 4. Ako su $x, y, z$ i $w$ pozitivni realni brojevi takvi da vrijedi\\
$$\cfrac{x}{y + z + w} + \cfrac{y}{z + w + x} + \cfrac{z}{w + x + y} +
\cfrac{w}{x + y + z} = 1 $$
odredi\\
$$\cfrac{x^2}{y + z + w} + \cfrac{y^2}{z + w + x} + \cfrac{z^2}{w + x + y} + \cfrac{w^2}{x + y + z}.$$
