Skup se može shvatiti kao bilo koja kolekcija različitih apstraktnih objekata smatranim cjelinom, a objekte koji čine skup nazivamo njegovim elementima. Dva primjera skupa su 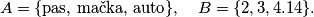
Neka su  i
i  skupovi. Za element
skupovi. Za element  iz skupa
iz skupa  pišemo
pišemo 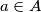 . Ako
. Ako  nije u skupu
nije u skupu  , pišemo
, pišemo 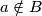 . Kažemo da je
. Kažemo da je  podskup od
podskup od  i pišemo
i pišemo 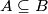 ako je svaki element skupa
ako je svaki element skupa  ujedno i element skupa
ujedno i element skupa  . Kažemo da su skupovi
. Kažemo da su skupovi  i
i  jednaki i pišemo
jednaki i pišemo 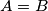 ako vrijedi
ako vrijedi 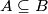 i
i 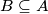 . Univerzalan skup je skup koji sadrži sve promatrane skupove.
. Univerzalan skup je skup koji sadrži sve promatrane skupove.
Sa skupovima možemo raditi sljedeće operacije: 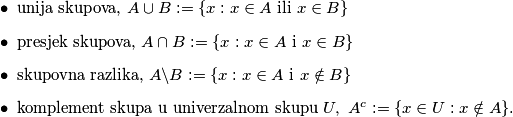
Kako bismo saznali odnos između dvaju ili više skupova, vrlo često ih grafički prikazujemo pomoću Vennovih dijagrama. Dolje je primjerice prikazan Vennov dijagram za presjek.
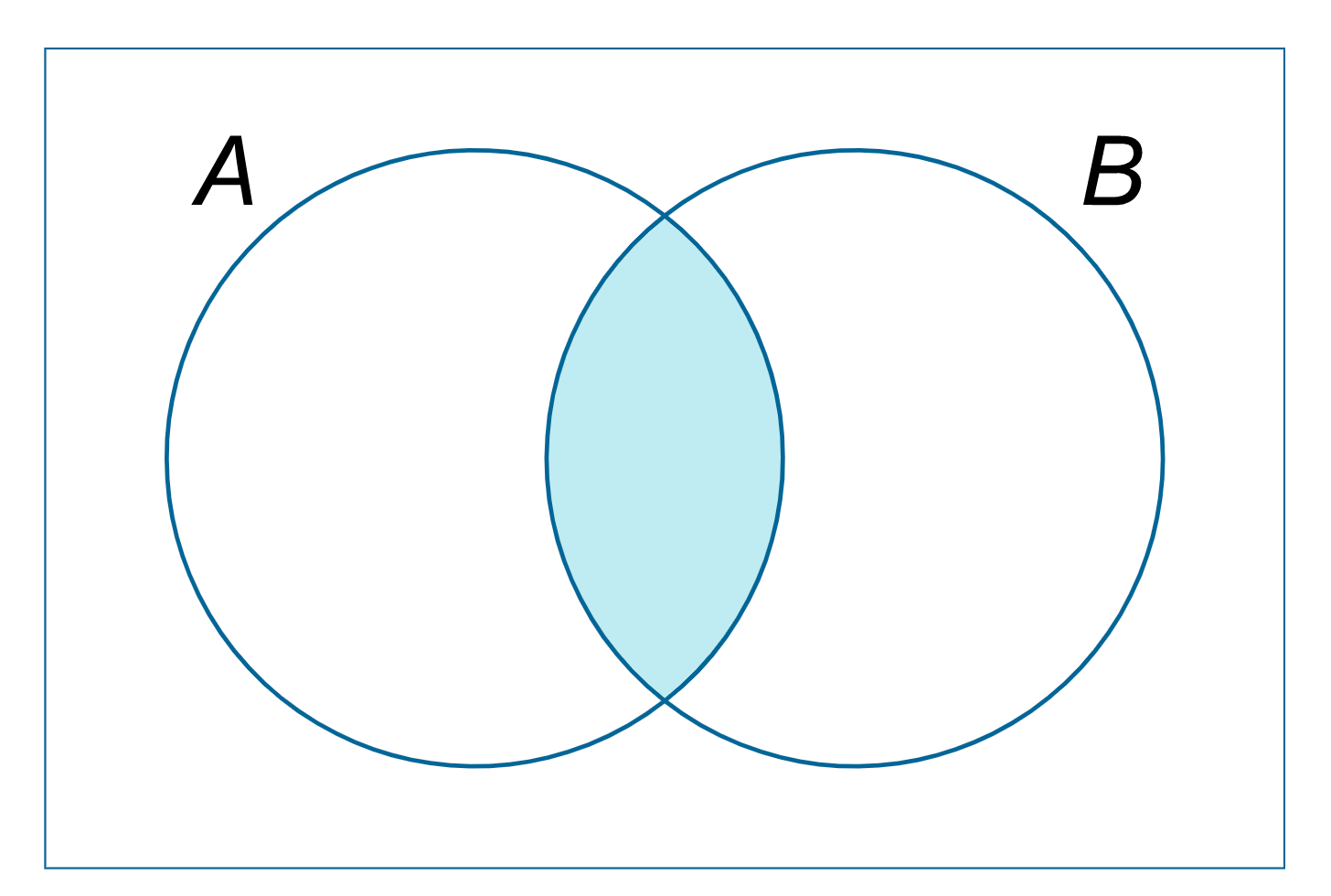
Na koncu, ipak treba izraziti jedan vrlo važan oprez. Naime, Vennovi dijagrami služe kao pomagalo za određivanje odnosa među skupovima, ali oni nisu formalni matematički dokaz uočenog odnosa. Pokažimo kako to radimo na primjeru. Neka je  univerzalan skup. Dokažimo da vrijedi
univerzalan skup. Dokažimo da vrijedi 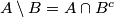 .
.
Uzmimo proizvoljan element 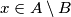 . To znači da je
. To znači da je 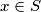 takav da
takav da 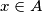 , ali
, ali 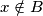 . Prema definiciji komplementa, imamo da je
. Prema definiciji komplementa, imamo da je 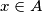 i
i 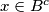 . Prema definiciji presjeka, dobivamo da je
. Prema definiciji presjeka, dobivamo da je 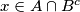 . Dakle, za prizvoljan
. Dakle, za prizvoljan 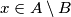 pokazali smo da se nalazi i u
pokazali smo da se nalazi i u 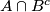 , stoga smo pokazali prema definiciji podskupa da vrijedi
, stoga smo pokazali prema definiciji podskupa da vrijedi 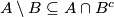 .
.
Obratno, uzmimo 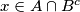 . Prema definiciji presjeka, imamo da je
. Prema definiciji presjeka, imamo da je 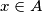 i
i 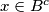 . Prema definiciji komplementa, vrijedi da je
. Prema definiciji komplementa, vrijedi da je 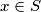 takav da
takav da 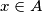 , ali
, ali 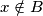 . Dakle, prema definiciji skupovne razlike, vrijedi
. Dakle, prema definiciji skupovne razlike, vrijedi 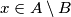 , stoga imamo
, stoga imamo 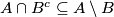 .
.
U konačnici, prema definiciji skupovne jednakosti dobivamo 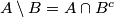 .
.
Unesite u prozor za rješenje  kako biste dobili
kako biste dobili  bod.
bod.
\textbf{Skup} se može shvatiti kao bilo koja kolekcija različitih apstraktnih objekata smatranim cjelinom, a objekte koji čine skup nazivamo njegovim \textbf{elementima}. Dva primjera skupa su
$$
A = \{ \text{pas, mačka, auto} \}, \quad B = \{ 2, 3, 4.14 \}.
$$
Neka su $A$ i $B$ skupovi. Za element $a$ iz skupa $A$ pišemo $a \in A$. Ako $a$ nije u skupu $B$, pišemo $a \notin B$. Kažemo da je $A$ \textbf{podskup} od $B$ i pišemo $A \subseteq B$ ako je svaki element skupa $A$ ujedno i element skupa $B$. Kažemo da su skupovi $A$ i $B$ \textbf{jednaki} i pišemo $A=B$ ako vrijedi $A \subseteq B$ i $B \subseteq A$. \textbf{Univerzalan skup} je skup koji sadrži sve promatrane skupove.
Sa skupovima možemo raditi sljedeće operacije:
\begin{itemize}
\item unija skupova, $A \cup B:=\{x : x \in A \text{ ili } x \in B\}$
\item presjek skupova, $A \cap B:=\{x : x \in A \text{ i } x \in B\}$
\item skupovna razlika, $A \backslash B:=\{x : x \in A \text{ i } x \notin B\}$
\item komplement skupa u univerzalnom skupu $U, \ A^c:=\{x \in U : x \notin A\}$.
\end{itemize}
Kako bismo saznali odnos između dvaju ili više skupova, vrlo često ih grafički prikazujemo pomoću \textbf{Vennovih dijagrama}. Dolje je primjerice prikazan Vennov dijagram za presjek.
\includegraphics{Slikazaslona2022-09-30u092049.png}
Na koncu, ipak treba izraziti jedan vrlo važan oprez. Naime, Vennovi dijagrami služe kao pomagalo za određivanje odnosa među skupovima, ali oni nisu formalni matematički dokaz uočenog odnosa. Pokažimo kako to radimo na primjeru. Neka je $S$ univerzalan skup. Dokažimo da vrijedi $A \setminus B = A \cap B^c$.
Uzmimo proizvoljan element $x \in A \setminus B$. To znači da je $x \in S$ takav da $x \in A$, ali $x \notin B$. Prema definiciji komplementa, imamo da je $x \in A$ i $x \in B^c$. Prema definiciji presjeka, dobivamo da je $x \in A \cap B^c$. Dakle, za prizvoljan $x \in A \setminus B$ pokazali smo da se nalazi i u $A \cap B^c$, stoga smo pokazali prema definiciji podskupa da vrijedi $A \setminus B \subseteq A \cap B^c$.
Obratno, uzmimo $x \in A \cap B^c$. Prema definiciji presjeka, imamo da je $x \in A$ i $x \in B^c$. Prema definiciji komplementa, vrijedi da je $x \in S$ takav da $x \in A$, ali $x \notin B$. Dakle, prema definiciji skupovne razlike, vrijedi $x \in A \setminus B$, stoga imamo $A \cap B^c \subseteq A \setminus B$.
U konačnici, prema definiciji skupovne jednakosti dobivamo $A \setminus B = A \cap B^c$.
Unesite u prozor za rješenje $1$ kako biste dobili $1$ bod.
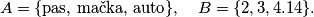
 i
i  skupovi. Za element
skupovi. Za element  iz skupa
iz skupa  pišemo
pišemo 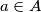 . Ako
. Ako  nije u skupu
nije u skupu  , pišemo
, pišemo 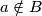 . Kažemo da je
. Kažemo da je  podskup od
podskup od  i pišemo
i pišemo 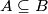 ako je svaki element skupa
ako je svaki element skupa  ujedno i element skupa
ujedno i element skupa  . Kažemo da su skupovi
. Kažemo da su skupovi  i
i  jednaki i pišemo
jednaki i pišemo 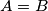 ako vrijedi
ako vrijedi 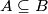 i
i 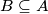 . Univerzalan skup je skup koji sadrži sve promatrane skupove.
. Univerzalan skup je skup koji sadrži sve promatrane skupove.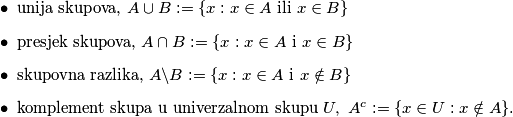

 univerzalan skup. Dokažimo da vrijedi
univerzalan skup. Dokažimo da vrijedi 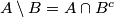 .
.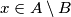 . To znači da je
. To znači da je 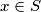 takav da
takav da 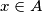 , ali
, ali 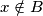 . Prema definiciji komplementa, imamo da je
. Prema definiciji komplementa, imamo da je 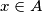 i
i 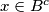 . Prema definiciji presjeka, dobivamo da je
. Prema definiciji presjeka, dobivamo da je 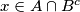 . Dakle, za prizvoljan
. Dakle, za prizvoljan 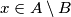 pokazali smo da se nalazi i u
pokazali smo da se nalazi i u 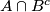 , stoga smo pokazali prema definiciji podskupa da vrijedi
, stoga smo pokazali prema definiciji podskupa da vrijedi 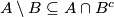 .
.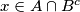 . Prema definiciji presjeka, imamo da je
. Prema definiciji presjeka, imamo da je 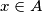 i
i 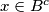 . Prema definiciji komplementa, vrijedi da je
. Prema definiciji komplementa, vrijedi da je 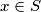 takav da
takav da 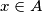 , ali
, ali 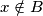 . Dakle, prema definiciji skupovne razlike, vrijedi
. Dakle, prema definiciji skupovne razlike, vrijedi 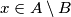 , stoga imamo
, stoga imamo 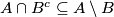 .
.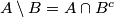 .
. kako biste dobili
kako biste dobili  bod.
bod. 