Vrijeme: 02:06

Skupovi - zadatak 3

Kad imamo uniju (odnosno presjek) više skupova, možemo izostaviti zagrade. 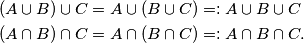\begin{aligned} &(A \cup B) \cup C=A \cup(B \cup C)=: A \cup B \cup C \\ &(A \cap B) \cap C=A \cap(B \cap C)=: A \cap B \cap C. \end{aligned} To se svojstvo zove asocijativnost. Za razliku od unije i presjeka, skupovna razlika nije asocijativna. Nadalje, presjek i unija su komutativne operacije, dok skupovna razlika nije, tj. 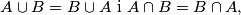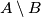vrijedi A \cup B=B \cup A \text { i } A \cap B=B \cap A, ali A \setminus B općenito nije jednako 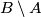B \setminus A. Ispitajte vrijedi li 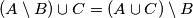(A \setminus B) \cup C=(A \cup C) \setminus B. Sve svoje tvrdnje dokažite.