Dirichletov princip je pravilo koje kaže da ako 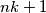 kuglicu stavimo u
kuglicu stavimo u  kutija, tada postoji barem jedna kutija u kojoj se nalazi barem
kutija, tada postoji barem jedna kutija u kojoj se nalazi barem  kuglica. Idemo dokazati tu tvrnju. Ako pretpostavimo suprotno, tj. da je u svakoj kutiji najviše
kuglica. Idemo dokazati tu tvrnju. Ako pretpostavimo suprotno, tj. da je u svakoj kutiji najviše  kuglica, onda je u svim kutijama zajedno najviše
kuglica, onda je u svim kutijama zajedno najviše 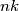 kuglica, a ima ih
kuglica, a ima ih 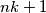 pa dolazimo do kontradikcije.
pa dolazimo do kontradikcije.
Ovu naizgled očitu tvrdnju (poznatu i kao princip kutija, princip golubinjaka, problem zečeva i kaveza i sl.) prvi je formalizirao njemački matematičar Johann Dirichlet 1834. godine. Cesto se javlja na državnim i županijskim natjecanjima. Na svu sreću već iz teksta zadatka može se naslutiti da je nužna primjena Dirichletova principa. Na to upućuju riječi kao što su barem, najmanje, postoji i dr. što ćemo vidjeti i u sljedećim primjerima.
Primjer 1: Dokažite da u skupini od  ljudi postoje barem
ljudi postoje barem  osobe koje su rođene u isto godišnje doba.
osobe koje su rođene u isto godišnje doba.
U ovom primjeru, kuglice su ljudi, dok su kutije godišnja doba. Primjetimo kako imamo 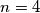 godišnjih doba i
godišnjih doba i 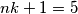 ljudi. Iz toga slijedi da je
ljudi. Iz toga slijedi da je 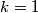 , pa prema Dirichletovom principu imamo kako barem jedna kutija sadrži
, pa prema Dirichletovom principu imamo kako barem jedna kutija sadrži 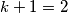 kuglice. Dakle, postoji godišnje doba u kojem su rođene barem dvije osobe. Promotrimo još jedan malo teži primjer.
kuglice. Dakle, postoji godišnje doba u kojem su rođene barem dvije osobe. Promotrimo još jedan malo teži primjer.
Primjer 2: U ladici je  pari čarapa. Bez gledanja izvlačimo jednu po jednu čarapu. Koliko čarapa moramo izvaditi iz ladice da bismo bili sigurni da imamo barem jedan par?
pari čarapa. Bez gledanja izvlačimo jednu po jednu čarapu. Koliko čarapa moramo izvaditi iz ladice da bismo bili sigurni da imamo barem jedan par?
U ovom primjeru, kuglice su čarape, dok su kutije par čarapa. Imamo 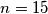 pari čarapa i želimo da barem jedna kutija ima
pari čarapa i želimo da barem jedna kutija ima 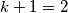 čarape. Dakle, vrijedi da je
čarape. Dakle, vrijedi da je 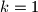 , pa prema Dirichletovom principu, minimalan broj čarapa potreban da budemo sigurni da imamo barem jedan par je
, pa prema Dirichletovom principu, minimalan broj čarapa potreban da budemo sigurni da imamo barem jedan par je 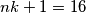 .
.
Unesite kao rezultat  da biste dobili bod.
da biste dobili bod.
\textbf{Dirichletov princip} je pravilo koje kaže da ako $n k+1$ kuglicu stavimo u $n$ kutija, tada postoji barem jedna kutija u kojoj se nalazi barem $k+1$ kuglica.
Idemo dokazati tu tvrnju. Ako pretpostavimo suprotno, tj. da je u svakoj kutiji najviše $k$ kuglica, onda je u svim kutijama zajedno najviše $n k$ kuglica, a ima ih $n k+1$ pa dolazimo do kontradikcije.
Ovu naizgled očitu tvrdnju (poznatu i kao princip kutija, princip golubinjaka, problem zečeva i kaveza i sl.) prvi je formalizirao njemački matematičar Johann Dirichlet 1834. godine. Cesto se javlja na državnim i županijskim natjecanjima. Na svu sreću već iz teksta zadatka može se naslutiti da je nužna primjena Dirichletova principa. Na to upućuju riječi kao što su barem, najmanje, postoji i dr. što ćemo vidjeti i u sljedećim primjerima.
\textbf{Primjer 1}: Dokažite da u skupini od $5$ ljudi postoje barem $2$ osobe koje su rođene u isto godišnje doba.
U ovom primjeru, \textit{kuglice} su ljudi, dok su \textit{kutije} godišnja doba. Primjetimo kako imamo $n = 4$ godišnjih doba i $nk
+ 1 = 5$ ljudi. Iz toga slijedi da je $k =1$, pa prema Dirichletovom principu imamo kako barem jedna kutija sadrži $k+1 = 2$ kuglice. Dakle, postoji godišnje doba u kojem su rođene barem dvije osobe. Promotrimo još jedan malo teži primjer.
\textbf{Primjer 2}: U ladici je $15$ pari čarapa. Bez gledanja izvlačimo jednu po jednu čarapu. Koliko čarapa moramo izvaditi iz ladice da bismo bili sigurni da imamo barem jedan par?
U ovom primjeru, \textit{kuglice} su čarape, dok su \textit{kutije} par čarapa. Imamo $n = 15$ pari čarapa i želimo da barem jedna kutija ima $k
+1 = 2$ čarape. Dakle, vrijedi da je $k = 1$, pa prema Dirichletovom principu, minimalan broj čarapa potreban da budemo sigurni da imamo barem jedan par je $nk
+ 1 = 16$.
Unesite kao rezultat $1$ da biste dobili bod.
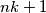 kuglicu stavimo u
kuglicu stavimo u  kutija, tada postoji barem jedna kutija u kojoj se nalazi barem
kutija, tada postoji barem jedna kutija u kojoj se nalazi barem  kuglica. Idemo dokazati tu tvrnju. Ako pretpostavimo suprotno, tj. da je u svakoj kutiji najviše
kuglica. Idemo dokazati tu tvrnju. Ako pretpostavimo suprotno, tj. da je u svakoj kutiji najviše  kuglica, onda je u svim kutijama zajedno najviše
kuglica, onda je u svim kutijama zajedno najviše 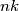 kuglica, a ima ih
kuglica, a ima ih 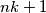 pa dolazimo do kontradikcije.
pa dolazimo do kontradikcije. ljudi postoje barem
ljudi postoje barem  osobe koje su rođene u isto godišnje doba.
osobe koje su rođene u isto godišnje doba.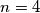 godišnjih doba i
godišnjih doba i 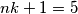 ljudi. Iz toga slijedi da je
ljudi. Iz toga slijedi da je 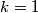 , pa prema Dirichletovom principu imamo kako barem jedna kutija sadrži
, pa prema Dirichletovom principu imamo kako barem jedna kutija sadrži 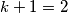 kuglice. Dakle, postoji godišnje doba u kojem su rođene barem dvije osobe. Promotrimo još jedan malo teži primjer.
kuglice. Dakle, postoji godišnje doba u kojem su rođene barem dvije osobe. Promotrimo još jedan malo teži primjer. pari čarapa. Bez gledanja izvlačimo jednu po jednu čarapu. Koliko čarapa moramo izvaditi iz ladice da bismo bili sigurni da imamo barem jedan par?
pari čarapa. Bez gledanja izvlačimo jednu po jednu čarapu. Koliko čarapa moramo izvaditi iz ladice da bismo bili sigurni da imamo barem jedan par?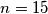 pari čarapa i želimo da barem jedna kutija ima
pari čarapa i želimo da barem jedna kutija ima 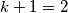 čarape. Dakle, vrijedi da je
čarape. Dakle, vrijedi da je 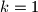 , pa prema Dirichletovom principu, minimalan broj čarapa potreban da budemo sigurni da imamo barem jedan par je
, pa prema Dirichletovom principu, minimalan broj čarapa potreban da budemo sigurni da imamo barem jedan par je 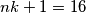 .
. da biste dobili bod.
da biste dobili bod. 