MetaMath '22

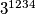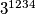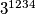\textbf{Primjer 1} \textit{(Larson 3.2.3)}: Koje su posljednje dvije znamenke broja $3^{1234}$? \textbf{Rješenje:}: Zanima nas koliko je $$3^{1234} \mod{100}$$ Postoji više načina kako dospjeti do $3^{1234}$, no obično počinjemo s manjim potencijama broja $3$ čije ostatke pri dijeljenju sa $100$ znamo pa koristimo prethodno navedena pravila da dođemo do $3^{1234}$. Koristit ćemo svojstva (b) i (c) Teorema 1. 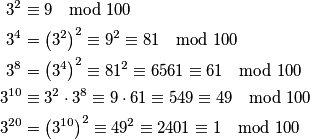\begin{align*} 3^2 &\equiv 9 \mod{100} \\ 3^4 &= \left( 3^2 \right)^2 \equiv 9^2 \equiv 81 \mod{100} \\ 3^8 &= \left( 3^4 \right)^2 \equiv 81^2 \equiv 6561 \equiv 61 \mod{100} \\ 3^{10} &\equiv 3^2 \cdot 3^8 \equiv 9\cdot 61 \equiv 549 \equiv 49 \mod{100}\\ 3^{20} & = \left( 3^{10}\right)^2 \equiv 49^2 \equiv 2401 \equiv 1 \mod{100} \end{align*} Budući da je 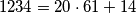$1234=20\cdot 61+14$, vrijedi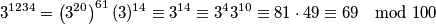 \[ 3^{1234}= \left( 3^{20} \right)^{61} (3)^{14} \equiv 3^{14} \equiv 3^43^{10}\equiv 81\cdot 49 \equiv 69 \mod{100} \] Dakle, posljednje dvije znamenke su 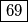$\boxed{69}$. Primijetimo da smo dobivši jedinicu u računu uboli prstom u pekmez. Ako je 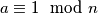$a \equiv 1 \mod{n}$, onda je i 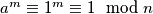$a^m\equiv 1^m\equiv 1 \mod{n}$. Zato u računu volimo dobiti $1$, $0$ ili $-1$. Pokušajte doći do odgovora i na barem jedan drugi način. Za nastavak, upišete odgovor, 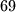$69$.